ГДЗ по Алгебре 7 Класс Номер 440 Дорофеев, Суворова — Подробные Ответы
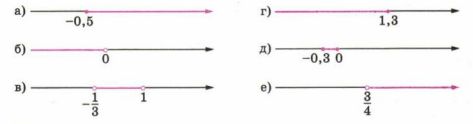
Работаем с символами Опишите на алгебраическом языке промежутки, изображённые на рисунке 5.7, a—е.
а) \( x \geq -0,5 \)
б) \( x < 0 \)
в) \( -\frac{1}{3} < x < 1 \)
г) \( x \leq 1,3 \)
д) \( -0,3 \leq x \leq 0 \)
е) \( x > \frac{3}{4} \)
а) \( x \geq -0,5 \) — Множество всех точек, которые больше либо равны -0,5.
Это множество представляет собой **закрытый интервал** \( [-0,5, +\infty) \), который включает все значения \( x \), начиная от -0,5 и продолжая вправо до бесконечности. Важно отметить, что точка \( x = -0,5 \) является частью множества, так как в неравенстве используется знак «больше либо равно». Такой интервал часто используется в математике и науке для обозначения диапазонов, где значения могут начинаться с конкретного порога (в данном случае -0,5), включая этот порог.
Множество включает все числа, начиная с -0,5 и дальше вправо, включая саму точку -0,5. Например, в физике или экономике такие интервалы могут быть использованы для представления диапазонов температур, доходов или других величин, которые могут начинаться с определенного значения.
б) \( x < 0 \) — Множество всех точек, которые строго меньше 0.
Это множество является **открытым интервалом** \( (-\infty, 0) \), который включает все значения \( x \), меньшие 0, но не включает саму точку 0. В задачах, где важно исключить определенное значение, например, значение 0, такой интервал является наиболее подходящим. Этот интервал может быть полезен, например, в экономике, когда рассматриваются убытки или отрицательные значения, где 0 не является частью решения задачи.
На координатной прямой этот интервал будет представлять собой все значения слева от 0, исключая саму точку 0. Это типичный пример использования открытых интервалов в математике и смежных областях.
в) \( -\frac{1}{3} < x < 1 \) — Множество всех точек, которые строго между -1/3 и 1, исключая эти точки.
Это множество представляет собой **открытый интервал** \( \left( -\frac{1}{3}, 1 \right) \), который включает все значения \( x \), строго больше -1/3 и строго меньше 1. Такие интервалы часто используются, когда важно исключить крайние значения, например, при решении задач с ограничениями, где граничные значения не могут быть включены в решение.
Этот интервал состоит из всех чисел между -1/3 и 1, но не включает эти граничные точки. В задачах с физическими или экономическими ограничениями, когда крайние значения не могут быть учтены, открытые интервалы играют важную роль. Например, такие интервалы могут быть использованы для представления диапазонов значений, которые не могут быть равны точкам границ, но могут находиться между ними.
г) \( x \leq 1,3 \) — Множество всех точек, которые меньше либо равны 1,3, включая саму точку \( x = 1,3 \).
Это множество является **закрытым интервалом** \( (-\infty, 1,3] \), которое включает все значения \( x \), которые меньше либо равны 1,3. Граничная точка \( x = 1,3 \) включена в множество, так как неравенство допускает равенство \( x = 1,3 \). Это полезно в задачах, где важна точка 1,3 как максимальное значение, и оно должно быть включено в решение. Например, такие интервалы могут быть использованы для расчета максимальных значений, таких как максимальная скорость, доход или температура.
Визуально этот интервал будет представлять собой все числа от минус бесконечности до 1,3, включая саму точку 1,3. Он часто используется для представления диапазонов значений, которые не могут превышать определенную величину, но могут быть равны этой величине.
д) \( -0,3 \leq x \leq 0 \) — Множество всех точек, которые больше либо равны -0,3 и меньше либо равны 0, включая эти точки.
Это множество представляет собой **закрытый интервал** \( [-0,3, 0] \), который включает все значения от -0,3 до 0, включая сами эти точки. Закрытые интервалы включают граничные значения, что делает их полезными для представления диапазонов, в которых важно учесть и крайние значения. Например, это может быть полезно при расчетах диапазонов температур или других величин, где важны как минимальные, так и максимальные значения.
На координатной прямой этот интервал будет представлять все числа от -0,3 до 0, включая эти две точки. Это полезно для задач, где важно учитывать как минимум и максимум в рамках решения задачи.
е) \( x > \frac{3}{4} \) — Множество всех точек, которые строго больше \( \frac{3}{4} \), исключая эту точку.
Это множество представляет собой **открытый интервал** \( \left( \frac{3}{4}, +\infty \right) \), который включает все значения \( x \), строго большие \( \frac{3}{4} \), но не включает саму точку \( x = \frac{3}{4} \). Открытые интервалы полезны, когда необходимо исключить определенные значения, такие как \( \frac{3}{4} \), и учесть все значения, которые находятся строго больше этой точки.
На координатной прямой этот интервал будет представлять все числа, которые больше \( \frac{3}{4} \), но не включает точку \( \frac{3}{4} \). Это может быть использовано, например, в задачах, связанных с диапазонами, где значения начинаются строго после определенной точки, исключая саму точку.