ГДЗ по Алгебре 7 Класс Номер 439 Дорофеев, Суворова — Подробные Ответы
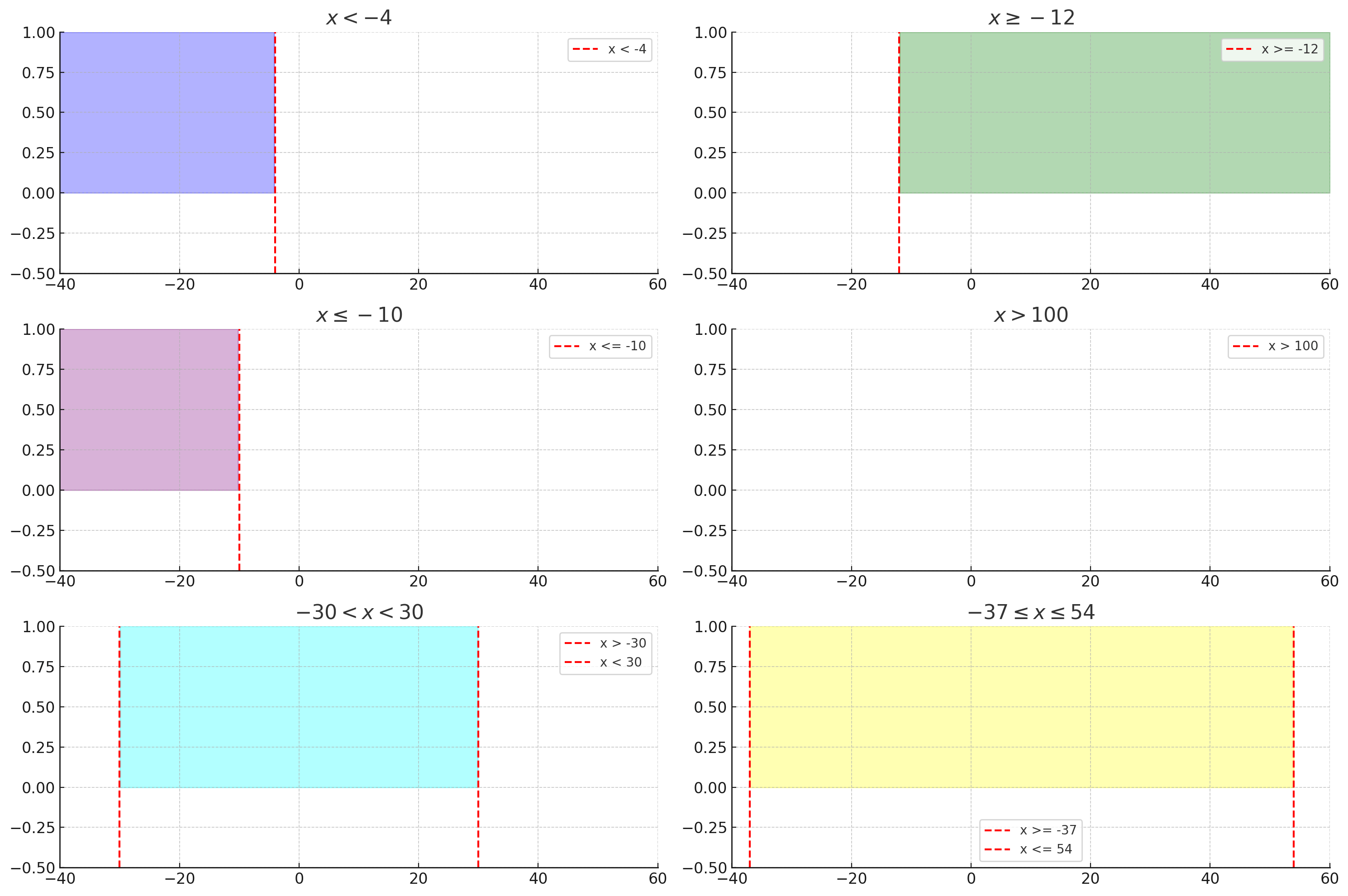
Изобразите на координатной прямой промежуток:
а) х < -4;
б) х > =-12;
в) х < = -10;
г) x > 100;
д) -30 < х < 30;
е) -37 < =х < =54.
а) \( x < -4 \) — Множество всех точек, которые находятся строго слева от точки \( x = -4 \).
Это множество включает все значения \( x \), которые меньше -4. Оно представляет собой **открытый интервал** \( (-\infty, -4) \), который не включает саму точку -4, но включает все числа, расположенные слева от этой точки. Такое множество используется, например, при решении задач, где важны все значения, меньшие определенной точки, но сама точка не должна быть включена.
б) \( x \geq -12 \) — Множество всех точек, которые больше либо равны -12, включая саму точку \( x = -12 \).
Это множество является **закрытым интервалом** \( [-12, +\infty) \). Оно включает все значения, начиная от -12 и далее вправо, включая саму точку -12. В задачах, где важно учесть все значения, начиная от конкретного порога, включая этот порог, такое множество часто используется.
в) \( x \leq -10 \) — Множество всех точек, которые меньше либо равны -10, включая саму точку \( x = -10 \).
Это множество также является **закрытым интервалом** \( (-\infty, -10] \), которое включает все значения \( x \), меньшие или равные -10. Такие интервалы часто используются в расчетах, где нужно учитывать все значения до определенного порога, включая этот порог.
г) \( x > 100 \) — Множество всех точек, которые строго больше 100.
Это множество является **открытым интервалом** \( (100, +\infty) \). Оно включает все значения \( x \), которые строго больше 100, исключая саму точку 100. Этот тип интервала используется, когда важны все значения, которые начинаются строго после некоторой точки.
д) \( -30 < x < 30 \) — Множество всех точек, которые строго между -30 и 30, не включая эти точки.
Это множество представляет собой **открытый интервал** \( (-30, 30) \), который не включает сами точки -30 и 30. Это множество состоит из всех чисел, которые лежат строго между этими двумя точками, но не включают их. Это типичный пример открытого интервала.
е) \( -37 \leq x \leq 54 \) — Множество всех точек, которые больше либо равны -37 и меньше либо равны 54, включая обе эти точки.
Это множество является **закрытым интервалом** \( [-37, 54] \), включающим все значения от -37 до 54, включая саму точку -37 и саму точку 54. Закрытые интервалы часто используются в случаях, когда крайние значения важны и должны быть учтены.
а) \( x < -4 \) — Множество всех точек, которые находятся строго слева от точки \( x = -4 \).
Это множество включает все значения \( x \), которые меньше -4. В математике такой промежуток называется **открытым интервалом** \( (-\infty, -4) \). Это означает, что интервал не включает саму точку \( x = -4 \), но охватывает все точки, которые расположены строго слева от неё. Например, это может быть полезно в задачах, где нужно учесть все значения, которые меньше определенной точки, но саму точку включать нельзя.
Если представить это на координатной прямой, то мы видим, что все значения от минус бесконечности до -4 принадлежат этому множеству. Однако сама точка \( x = -4 \) исключена, так как она не удовлетворяет неравенству \( x < -4 \). Это может быть использовано, например, при анализе диапазонов значений, где крайние значения не имеют значения (например, температурный диапазон, исключающий точку замерзания воды).
б) \( x \geq -12 \) — Множество всех точек, которые больше либо равны -12, включая саму точку \( x = -12 \).
Это множество представляет собой **закрытый интервал** \( [-12, +\infty) \), так как оно включает все значения \( x \), начиная с -12 и продолжая вправо до бесконечности. В данном случае граничная точка \( x = -12 \) включена в множество, так как неравенство допускает равенство \( x = -12 \). Множество таких точек часто используется, когда важно учесть границу, начиная с которой все последующие значения принадлежат решению задачи. Например, в задачах, где необходимо учесть минимальные возможные значения, начиная с определённого порога, этот интервал будет наиболее подходящим.
Визуально это множество будет выглядеть как область на координатной прямой, начиная с точки \( x = -12 \) и продолжающаяся вправо, включая все значения, которые больше или равны -12. Этот интервал применяется в задачах, где важен предел или минимальная точка отсчета, например, в расчетах времени или расстояний.
в) \( x \leq -10 \) — Множество всех точек, которые меньше либо равны -10, включая саму точку \( x = -10 \).
Это множество также является **закрытым интервалом** \( (-\infty, -10] \), так как оно включает все значения \( x \), меньшие или равные -10. Включение точки \( x = -10 \) важно в случаях, когда необходимо учесть крайнее значение. Например, это может быть важно при расчетах, где значения до определенной границы включаются в расчет, а сама граница (в данном случае -10) является важным элементом для решения задачи.
Этот интервал представляет собой все точки, которые находятся слева от точки \( x = -10 \), включая саму точку -10. Он может быть использован, например, в задачах, где рассматриваются ограничения, которые включают как минимум до определенной границы, или когда необходимо учесть все значения, не превышающие заданного максимума.
г) \( x > 100 \) — Множество всех точек, которые строго больше 100.
Это множество представляет собой **открытый интервал** \( (100, +\infty) \). Оно включает все значения \( x \), которые строго больше 100, но не включает саму точку \( x = 100 \). Это может быть полезно в задачах, где нужно учитывать значения, которые начинаются после определенной точки, исключая саму точку. Например, в расчетах, связанных с числовыми порогами или величинами, которые могут начинаться только после определенного значения.
На координатной прямой этот интервал будет представлять все точки, начиная с 100 и далее, но точка 100 в этом интервале не будет включена. Это типичный пример использования открытых интервалов, где важно исключить крайние значения.
д) \( -30 < x < 30 \) — Множество всех точек, которые строго между -30 и 30, не включая эти точки.
Это множество представляет собой **открытый интервал** \( (-30, 30) \), который включает все значения между -30 и 30, но не включает сами точки -30 и 30. Такое множество используется, например, в задачах, где важно учесть диапазон значений, исключая самую границу, например, при измерениях, когда важно не допускать значения, равные границам диапазона.
Этот интервал отображает все числа, которые лежат строго между точками -30 и 30, но саму точку -30 и 30 исключает. Это можно использовать, например, для учета всех значений, которые лежат в пределах определенной области, но крайние значения этой области не должны быть включены.
е) \( -37 \leq x \leq 54 \) — Множество всех точек, которые больше либо равны -37 и меньше либо равны 54, включая обе эти точки.
Это множество представляет собой **закрытый интервал** \( [-37, 54] \), который включает все значения от -37 до 54, включая обе граничные точки. Такие множества часто используются, когда важно учесть все значения в пределах определенного диапазона, включая его границы. Например, это может быть полезно при анализе данных, где границы интервала важны и должны быть включены для точности расчетов.
Визуально на координатной прямой этот интервал будет охватывать все точки от -37 до 54, включая эти две точки. Это характерно для задач, где нужно включить все возможные значения, которые могут быть равны этим граничным точкам.