ГДЗ по Алгебре 7 Класс Номер 438 Дорофеев, Суворова — Подробные Ответы
Изобразите на координатной прямой множество точек, координаты которых удовлетворяют двойному неравенству:
а) 4 < = x < = 10;
б) -15 < = x < = 27;
в) 8 < х < 11.
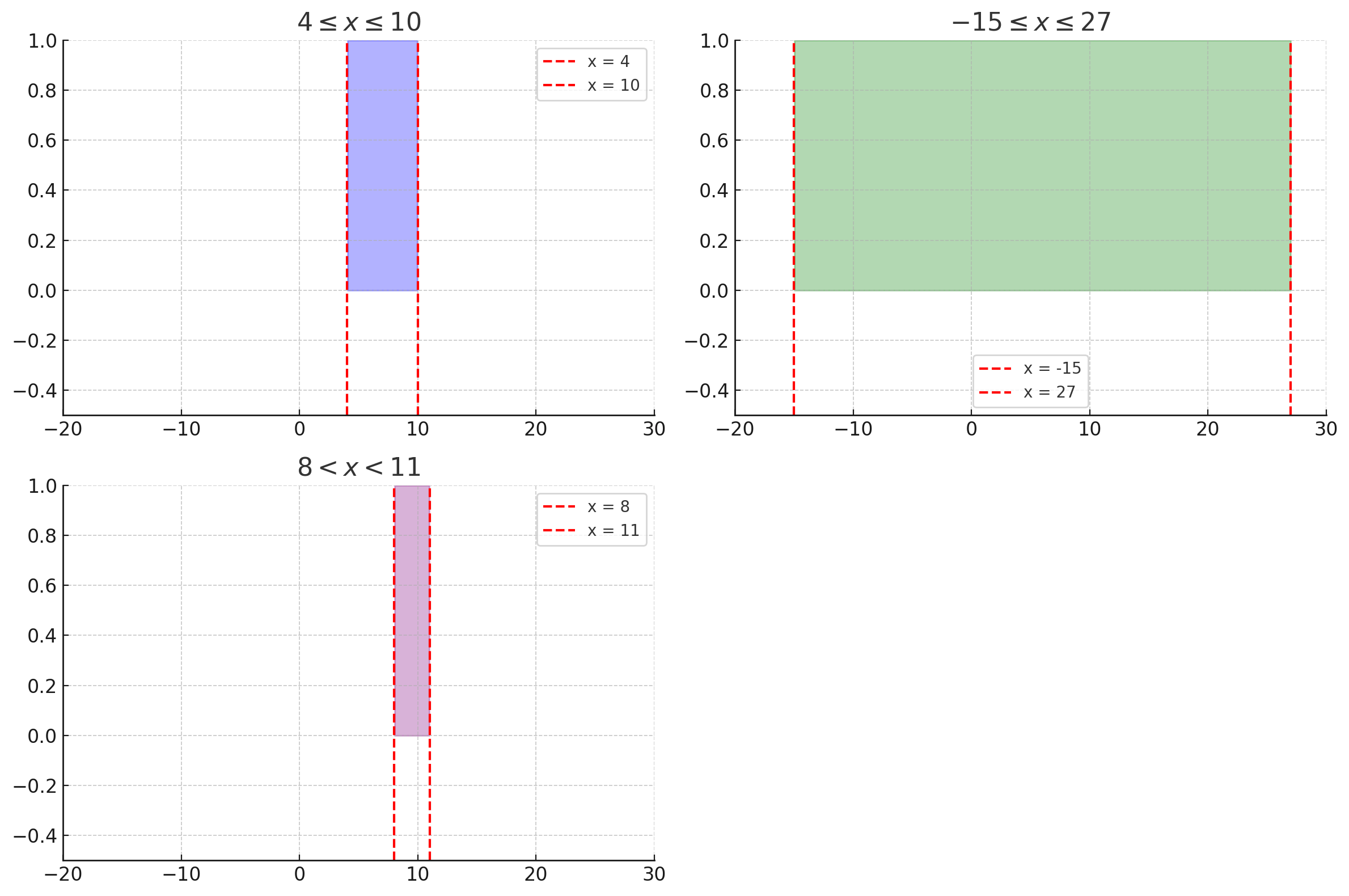
а) \( 4 \leq x \leq 10 \) — Множество всех точек, расположенных между 4 и 10, включая обе эти точки.
Это множество представляет собой **закрытый интервал** \( [4, 10] \). Интервал включает все значения \( x \), начиная от 4 и заканчивая 10, включая сами эти точки. То есть, \( x = 4 \) и \( x = 10 \) также являются элементами множества. Такое множество используется, например, когда важно включить оба конца интервала, что может быть полезно в задачах, где крайние значения имеют значение.
б) \( -15 \leq x \leq 27 \) — Множество всех точек, расположенных между -15 и 27, включая эти точки.
Это множество также является **закрытым интервалом** \( [-15, 27] \), включающим обе граничные точки: -15 и 27. Важно, что в этом интервале значения \( x \) могут быть как отрицательными, так и положительными, но все значения между -15 и 27, включая эти крайние точки, принадлежат множеству. Это множество часто встречается в задачах, где есть ограничения на максимальные и минимальные значения.
в) \( 8 < x < 11 \) — Множество всех точек, расположенных строго между 8 и 11, исключая эти точки.
Это множество представляет собой **открытый интервал** \( (8, 11) \), который не включает сами точки 8 и 11. Оно состоит только из тех значений \( x \), которые строго больше 8 и строго меньше 11. Открытые интервалы используются, когда нужно исключить граничные значения, например, при решении задач с ограничениями, которые не включают крайние значения.
а) \( 4 \leq x \leq 10 \) — Множество всех точек, расположенных между 4 и 10, включая обе эти точки.
Это множество представляет собой **закрытый интервал** \( [4, 10] \). В этом интервале значения \( x \) могут быть любыми числами от 4 до 10, включая как 4, так и 10. Важно заметить, что **закрытый интервал** означает, что обе граничные точки, 4 и 10, включены в множество. Такие множества часто встречаются в задачах, где необходимо учесть как минимальное, так и максимальное значение. Например, это может быть полезно при решении задач, где важно учитывать крайние значения (например, в расчетах, где 4 и 10 — это важные пороговые значения).
Если представить это множество на координатной прямой, то оно будет включать все значения, начиная с 4 и заканчивая 10, причем точки 4 и 10 тоже будут являться частью множества. Для этого можно сказать, что \( x \in [4, 10] \), и это множество всех значений, которые лежат между этими точками, включая их.
б) \( -15 \leq x \leq 27 \) — Множество всех точек, расположенных между -15 и 27, включая эти точки.
Это множество также представляет собой **закрытый интервал** \( [-15, 27] \), который включает все значения \( x \), начиная от -15 и заканчивая 27. В данном случае граничные точки, -15 и 27, также принадлежат множеству, так как это **закрытый интервал**. Множество содержит все числа, которые могут быть как отрицательными, так и положительными, но обязательно включает и -15, и 27. Такой тип интервала часто используется в ситуациях, когда важно включить крайние значения. Например, это может быть полезно в расчетах, где важно учесть минимальные и максимальные возможные значения (например, если мы рассматриваем диапазон температур или доходов, где пределы должны быть включены).
Этот интервал имеет следующий вид: \( x \in [-15, 27] \), что означает, что все значения от -15 до 27, включая их, принадлежат этому множеству.
в) \( 8 < x < 11 \) — Множество всех точек, расположенных строго между 8 и 11, исключая эти точки.
Это множество представляет собой **открытый интервал** \( (8, 11) \), который не включает сами точки 8 и 11, но включает все значения между ними. Открытый интервал означает, что граничные точки \( x = 8 \) и \( x = 11 \) не принадлежат множеству, но все числа между ними являются частью множества. Например, это может быть полезно в задачах, где граничные значения не могут быть включены, например, при расчетах, где определенные значения исключаются.
На координатной прямой этот интервал будет представлять собой все числа, которые лежат строго между точками 8 и 11, но не включая эти точки. То есть, мы будем рассматривать значения \( x \in (8, 11) \), и этот интервал исключает сами 8 и 11.
Открытые интервалы широко используются в математике, например, при нахождении промежутков, где значения могут быть только в пределах строго ограниченного диапазона, исключая крайние значения. Это может быть полезно, например, при работе с нестрогими ограничениями или в задачах, где нужно исключить точные граничные значения.