ГДЗ по Алгебре 7 Класс Номер 437 Дорофеев, Суворова — Подробные Ответы
Изобразите на координатной прямой множество всех точек:
а) с отрицательными координатами;
б) с неотрицательными координатами.
Задайте каждое из этих множеств с помощью неравенства.
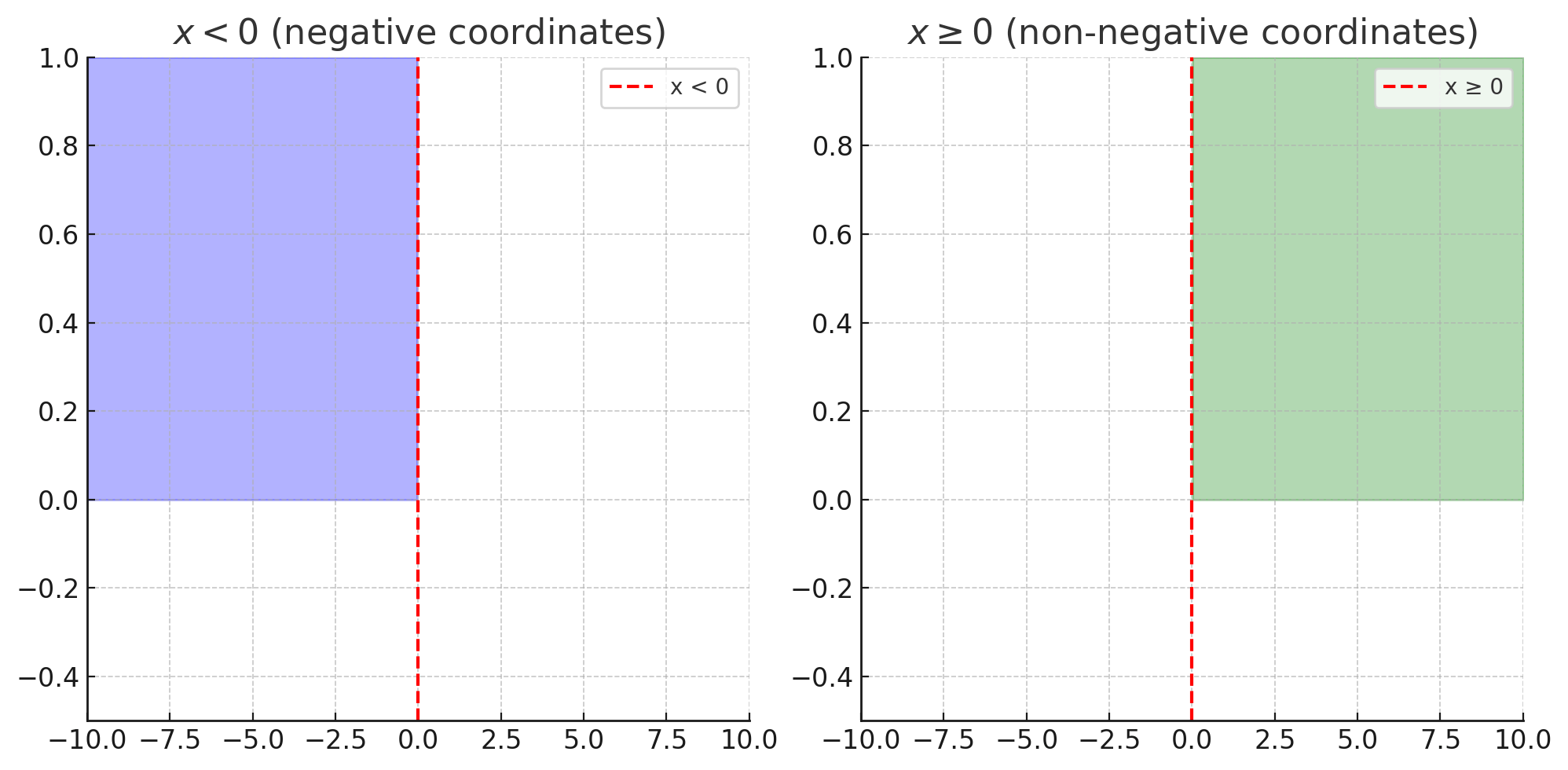
a) \( x < 0 \) — Множество всех точек с отрицательными координатами.
Это множество включает все значения \( x \), которые меньше 0. Оно отображается как открытый интервал \( (-\infty, 0) \), то есть все значения, которые расположены слева от точки 0, являются частью этого множества. Это множество называется **открытым интервалом**, так как не включает саму точку \( x = 0 \).
б) \( x \geq 0 \) — Множество всех точек с неотрицательными координатами.
Это множество включает все значения \( x \), которые больше либо равны 0. Оно отображается как закрытый интервал \( [0, +\infty) \), то есть все значения, начиная с 0 и дальше вправо, принадлежат этому множеству. Это множество называется **закрытым интервалом**, так как включает саму точку \( x = 0 \).
a) \( x < 0 \) — Множество всех точек с отрицательными координатами.
Это множество включает все значения \( x \), которые меньше 0. В математике такие множества называются **открытыми интервалами**, потому что они не включают границу. В данном случае точка \( x = 0 \) не является частью множества, так как условие строгое (\( x < 0 \)). Это означает, что множество состоит только из точек, расположенных слева от 0, но не включает саму точку 0. Визуально это можно представить как область на координатной прямой, которая начинается от минус бесконечности и продолжается до, но не включая, точки 0.
Множество всех точек, которые меньше нуля, можно выразить как открытый интервал \( (-\infty, 0) \). Этот интервал включает все значения от минус бесконечности до 0, но саму точку 0 не включает. Это множество широко используется в различных задачах, где необходимо работать только с отрицательными числами. Например, в задачах, связанных с отрицательными величинами, такими как температура ниже нуля или убытки в финансовых расчетах.
б) \( x \geq 0 \) — Множество всех точек с неотрицательными координатами.
Это множество включает все значения \( x \), которые больше либо равны 0. В отличие от предыдущего случая, здесь мы включаем в множество саму точку \( x = 0 \), так как неравенство \( x \geq 0 \) позволяет взять значение 0. Такое множество называется **закрытым интервалом**, поскольку оно включает и граничную точку, в отличие от открытого интервала, где граница исключена.
Визуально это множество представляется как область на координатной прямой, которая начинается от точки 0 и продолжается до плюс бесконечности. Включение точки 0 в это множество важно, так как она представляет собой минимальное значение на данной прямой, и в некоторых задачах мы не можем исключать эту точку. Например, если речь идет о физических величинах, таких как расстояние или время, где отрицательные значения не имеют смысла, то нам важно включить 0, как минимальное возможное значение.
Множество всех точек, которые больше либо равны нулю, можно выразить как закрытый интервал \( [0, +\infty) \). Этот интервал включает все значения от 0 до плюс бесконечности и саму точку 0. Этот интервал часто используется в задачах, связанных с ограничениями, где необходимо включить минимальное значение, например, в расчетах, связанных с минимальными требованиями или пороговыми значениями.