ГДЗ по Алгебре 7 Класс Номер 436 Дорофеев, Суворова — Подробные Ответы

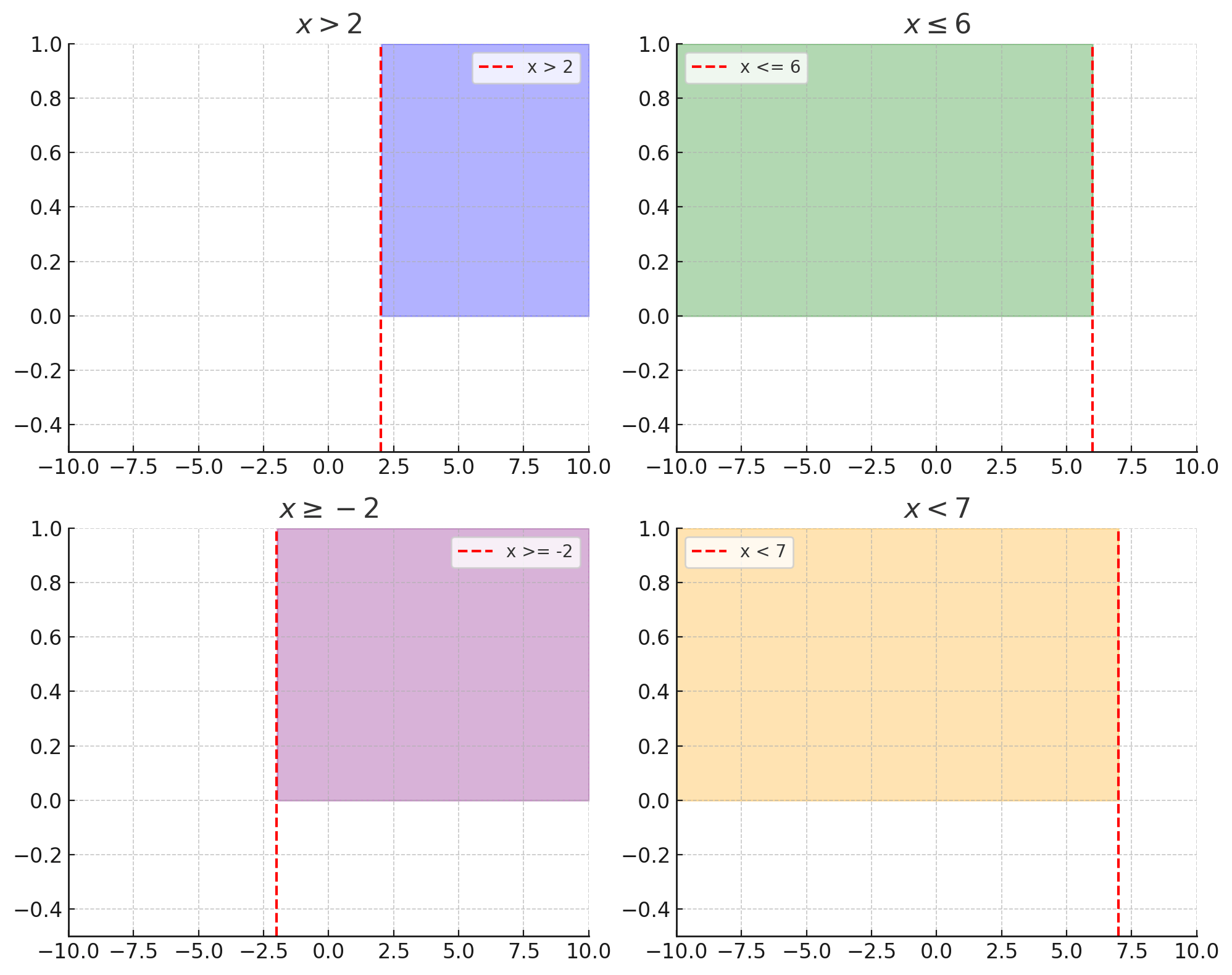
Изобразите на координатной прямой множество точек, заданное неравенством: а) х > б; б) х < =6; в) х > =-2; г) х < 7. Как называется каждое из этих множеств?

На графике изображены множества точек, заданные неравенствами:

1. $x > 2$ — Множество всех точек, расположенных справа от точки $x = 2$. Это множество называется открытым интервалом.

2. $x \leq 6$ — Множество всех точек, расположенных слева от точки $x = 6$ и включающая саму точку $x = 6$. Это множество называется закрытым интервалом.

3. $x \geq -2$ — Множество всех точек, расположенных справа от точки $x = -2$ и включая саму точку $x = -2$. Это множество называется закрытым интервалом.

4. $x < 7$ — Множество всех точек, расположенных слева от точки $x = 7$. Это множество называется открытым интервалом.

• $x > 2$ — Множество всех точек, расположенных справа от точки $x = 2$.

  Это множество включает все значения $x$, которые больше, чем 2. Оно не включает саму точку $x = 2$, так как в данном случае неравенство строгое. Мы говорим, что это множество является открытым интервалом. Множество не включает правую границу, и вся область справа от точки 2 будет частью этого множества. Это часто используют, когда хотят подчеркнуть, что начальная точка (в данном случае $x = 2$) не включается в решение.

  Пример:

  $$x>2\text{означает, что}x\in (2,+\mathrm{\infty })$$

  Это множество всех точек, которые больше 2, начиная с 2, но без её включения.

• $x \leq 6$ — Множество всех точек, расположенных слева от точки $x = 6$ и включающее саму точку $x = 6$.

  Здесь неравенство включает как все значения $x$, меньшие или равные 6, так и саму точку $x = 6$. Множество всех таких значений называется закрытым интервалом. Важно отметить, что в данном случае мы включаем саму точку 6, то есть она является частью множества. Это характерно для случаев, когда нужно включить граничные значения, например, в задачах, связанных с пределами, или при учёте ограничений.

  Пример:

  $$x\le 6\text{означает, что}x\in (-\mathrm{\infty },6]$$

  Это множество всех точек, которые меньше или равны 6, включая саму точку 6.

• $x \geq -2$ — Множество всех точек, расположенных справа от точки $x = -2$, и включая саму точку $x = -2$.

  В этом случае неравенство включает все значения $x$, которые больше либо равны -2. Множество включает саму точку $x = -2$, и такое множество называется закрытым интервалом. Когда мы говорим $x \geq -2$, это значит, что все значения, начиная от -2 и далее, являются частью множества, включая саму точку -2. Это можно применить в задачах, где важно учесть граничные значения и обеспечить их включение.

  Пример:

  $$x\ge -2\text{означает, что}x\in [-2,+\mathrm{\infty })$$

  Это множество всех точек, которые больше или равны -2, включая саму точку -2.

• $x < 7$ — Множество всех точек, расположенных слева от точки $x = 7$.

  В данном случае неравенство не включает саму точку $x = 7$, а охватывает все значения $x$, которые меньше 7. Это множество называется открытым интервалом, так как мы не включаем точку $x = 7$ в множество. Важно, что это множество включает все значения, которые строго меньше 7, и вся область слева от этой точки является частью множества.

  Пример:

  $$x<7\text{означает, что}x\in (-\mathrm{\infty },7)$$

  Это множество всех точек, которые меньше 7, не включая саму точку 7.