ГДЗ по Алгебра 7 Класс Номер 319 Дорофеев, Суворова — Подробные Ответы
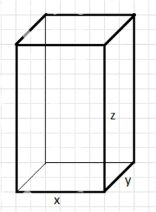
Как можно истолковать на «языке объёмов» равенство
(xy)z = x(yz)?
\( (xy)z = x(yz) \)
Чтобы найти объем прямоугольного параллелепипеда, можно сначала найти площадь нижнего основания и умножить все на \( z \); или найти площадь боковой грани и умножить все на \( x \).
1) Формула для нахождения объема прямоугольного параллелепипеда выглядит следующим образом:
\( (xy)z = x(yz) \)
Здесь \( x \), \( y \) и \( z \) — это длина, ширина и высота параллелепипеда соответственно. Для вычисления объема прямоугольного параллелепипеда нужно учитывать его размеры по всем трем осям.
2) Чтобы найти объем прямоугольного параллелепипеда, можно выполнить несколько шагов в зависимости от того, как мы подходим к решению задачи:
— Во-первых, можно начать с нахождения площади нижнего основания параллелепипеда. Площадь основания равна произведению длины и ширины, то есть \( xy \). После этого нужно умножить полученную площадь на высоту \( z \), чтобы получить объем:
\( (xy)z \), где \( xy \) — это площадь основания, а \( z \) — высота. Таким образом, объем равен \( xy \cdot z \).
— Во-вторых, можно вычислить объем, умножив площадь боковой грани на длину. Площадь боковой грани равна произведению высоты на ширину, то есть \( yz \). После этого нужно умножить полученную площадь на длину \( x \), чтобы получить объем:
\( x(yz) \), где \( yz \) — это площадь боковой грани, а \( x \) — длина. Таким образом, объем равен \( x \cdot yz \).
3) Оба метода дадут одинаковый результат, так как оба выражения \( (xy)z \) и \( x(yz) \) равны по сути. Это объясняется ассоциативным свойством умножения, которое позволяет переставлять скобки, не меняя результата умножения.
4) Таким образом, объем прямоугольного параллелепипеда можно найти двумя способами, используя разные подходы, но результат будет одинаковым.
Ответ: объем прямоугольного параллелепипеда можно найти как \( (xy)z \) или \( x(yz) \), в зависимости от того, какой параметр мы выберем первым для вычислений.