ГДЗ по Алгебра 7 Класс Номер 317 Дорофеев, Суворова — Подробные Ответы
Верно ли, что (х — y)z = xz — yz?
Дайте истолкование этого равенства на «языке площадей».
\( (x — y)z = xz — yz \)
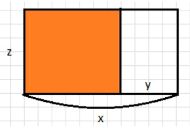
Чтобы найти площадь закрашенного прямоугольника, надо ширину \( z \) умножить на длину \( (x — y) \),
или из площади всего прямоугольника \( xz \) вычесть площадь незакрашенного прямоугольника.
В этой задаче рассматривается нахождение площади закрашенного прямоугольника, где один из углов прямоугольника вычитается из общей площади. Рассмотрим шаги для нахождения площади закрашенной части:
1) У нас есть выражение \( (x — y)z = xz — yz \). Это уравнение выражает площадь закрашенного прямоугольника, где \( x \) — длина всего прямоугольника, \( y \) — длина незакрашенной части, а \( z \) — ширина прямоугольника.
2) Чтобы найти площадь закрашенного прямоугольника, нужно ширину \( z \) умножить на длину закрашенной части прямоугольника, которая равна \( (x — y) \). Таким образом, площадь закрашенного прямоугольника будет:
\( \text{Площадь} = z \times (x — y) \).
3) Альтернативный способ нахождения площади закрашенной части — это вычислить площадь всего прямоугольника \( xz \), а затем вычесть площадь незакрашенной части, которая равна \( yz \). То есть:
\( \text{Площадь закрашенного прямоугольника} = xz — yz \).
4) Таким образом, мы пришли к двум эквивалентным формулам для нахождения площади закрашенного прямоугольника. Это показывает, что вычитаемая часть из общей площади прямоугольника равна площади незакрашенной части, а оставшаяся часть является закрашенной.
Ответ: Площадь закрашенного прямоугольника можно вычислить по любой из предложенных формул, в зависимости от доступных данных: \( z \times (x — y) \) или \( xz — yz \).