ГДЗ по Алгебра 7 Класс Номер 289 Дорофеев, Суворова — Подробные Ответы
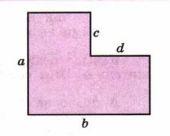
Запишите выражения для вычисления площади фигуры (рис. 3.9) сначала сложением площадей прямоугольников, а затем вычитанием. Покажите, как можно получить второе выражение из первого с помощью преобразований.
1) Площадь фигуры, сложением площадей прямоугольников:
\( (b — d)c + (a — c)b \)
2) Площадь фигуры, вычитанием площадей прямоугольников:
\( ab — cd \)
3) Второе выражение из первого получается:
\( (b — d)c + (a — c)b = bc — cd + ab — bc = ab — cd \)
1) Площадь фигуры, сложением площадей прямоугольников:
В данном случае площадь фигуры можно выразить через два прямоугольника. Первый прямоугольник имеет размеры \( (b — d) \) и \( c \), а второй — \( (a — c) \) и \( b \). Площадь первого прямоугольника равна \( (b — d) \cdot c \), а второго — \( (a — c) \cdot b \). Общая площадь фигуры будет равна сумме площадей этих прямоугольников, то есть:
\( (b — d)c + (a — c)b \).
2) Площадь фигуры, вычитанием площадей прямоугольников:
Во втором случае площадь фигуры можно выразить через один прямоугольник с размерами \( a \) и \( b \), из которого вычитаем площадь двух прямоугольников: первый прямоугольник имеет размеры \( d \) и \( c \), второй — \( c \) и \( b \). Тогда общая площадь фигуры равна:
\( ab — cd \).
3) Второе выражение из первого получается:
Теперь давайте преобразуем первое выражение, используя алгебраические преобразования. Мы имеем:
\( (b — d)c + (a — c)b = bc — cd + ab — bc \).
Теперь видим, что \( bc — bc = 0 \), и остается:
\( ab — cd \).
Таким образом, оба способа вычисления площади дают одинаковый результат: \( ab — cd \).