ГДЗ по Алгебра 7 Класс Номер 280 Дорофеев, Суворова — Подробные Ответы

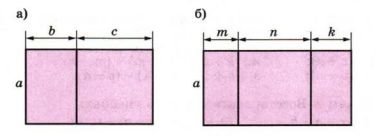
Составьте два выражения для вычисления площади фигуры (рис. 3.8, а, б) и покажите, как одно из этих выражений можно преобразовать в другое.

a) \( S = ab + ac; \, S = a(b + c); \)

\( a(b + c) = ab + ac. \)

б) \( S = am + an + ak; \, S = a(m + n + k); \)

\( a(m + n + k) = am + an + ak. \)

a) Рассмотрим первое выражение \( S = ab + ac \), где \( S \) — это выражение для площади или некоторой суммы, зависящей от переменных \( a \), \( b \) и \( c \). Это выражение говорит нам, что сумма двух произведений (между \( a \) и \( b \), а также \( a \) и \( c \)) дает общее значение \( S \). Также можно выразить это как \( S = a(b + c) \), что является распределением множителя \( a \) по сумме \( (b + c) \). Это математическое свойство называется распределительным законом умножения относительно сложения, и оно показывает, как одно произведение можно преобразовать в сумму двух других произведений.

Следовательно, если мы раскрываем скобки в \( a(b + c) \), то получаем: \( a(b + c) = ab + ac \), что возвращает нас к исходному выражению \( S = ab + ac \). Этот шаг демонстрирует, как умножение на сумму может быть перераспределено через распределительный закон, что делает более удобным упрощение или преобразование выражений в дальнейшем.

Ответ: \( S = ab + ac; \, S = a(b + c); \) и \( a(b + c) = ab + ac \).

б) В следующем выражении \( S = am + an + ak \), мы видим, что это расширение предыдущего шага, где \( a \) умножается на три различные переменные \( m \), \( n \) и \( k \). Мы можем снова применить распределительный закон умножения, чтобы записать это как \( S = a(m + n + k) \). Здесь мы видим, что сумма переменных \( m \), \( n \) и \( k \) объединена в одну скобку, и затем умножена на \( a \). Этот подход позволяет более компактно записать выражение, особенно если \( a \) является общим множителем для всех переменных.

Далее, раскрывая скобки в \( a(m + n + k) \), мы получаем: \( a(m + n + k) = am + an + ak \), что возвращает нас к исходной форме выражения \( S = am + an + ak \). Это подтверждает, что при распределении множителя \( a \) через сумму, результат будет эквивалентен изначальному выражению.

Ответ: \( S = am + an + ak; \, S = a(m + n + k); \) и \( a(m + n + k) = am + an + ak \).