ГДЗ по Алгебра 7 Класс Номер 271 Дорофеев, Суворова — Подробные Ответы

Составьте формулу для вычисления площади S фигуры (рис. 3.7, а, б).

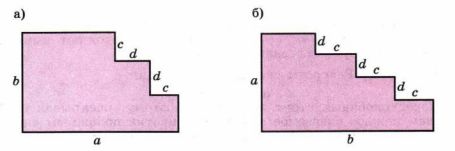
а) Формула: S = ab — cd — c(c + d)

Шаг 1: Начнем с того, что выражение S состоит из площади большого прямоугольника ab и вычитания площадей небольших прямоугольников, выраженных через cd и c(c + d).

Шаг 2: Раскроем скобки в выражении c(c + d):

S = ab — cd — c² — cd

Шаг 3: Приводим подобные слагаемые. Площадь двух прямоугольников cd суммируется, и получается:

S = ab — 2cd — c²

Итог: Для первой фигуры мы получаем следующее выражение для площади:

• S = ab — 2cd — c²

б) Формула: S = ab — cd — c(d + d) — c(d + d + d)

Шаг 1: Как и в первом случае, начнем с площади большого прямоугольника ab и вычитания площадей меньших прямоугольников. Мы видим, что cd вычитается дважды, а выражения c(d + d) и c(d + d + d) представляют площади ступеней прямоугольников.

Шаг 2: Раскрываем скобки в выражениях c(d + d) и c(d + d + d):

S = ab — cd — c · 2d — c · 3d

Шаг 3: Теперь приводим подобные слагаемые. Мы видим, что у нас есть три вычитания площадей прямоугольников с размерами cd, 2cd, и 3cd:

S = ab — cd — 2cd — 3cd

Шаг 4: Упрощаем выражение, суммируя все вычитания площадей прямоугольников:

S = ab — 6cd

Итог: Для второй фигуры мы получаем следующее выражение для площади:

• S = ab — 6cd

а)

S = ab — cd — c(c + d)

Шаг 1: Начальная формула представляет собой площадь, где ab — это площадь большого прямоугольника, а остальные элементы содержат площади небольших прямоугольников, которые вычитаются.

Раскрываем скобки в выражении c(c + d):

S = ab — cd — c² — cd

Шаг 2: Приводим подобные слагаемые:

S = ab — 2cd — c²

Таким образом, мы получили выражение для площади S, где ab — площадь большого прямоугольника, а 2cd и c² — площади меньших прямоугольников.

б)

S = ab — cd — c(d + d) — c(d + d + d)

Шаг 1: В этом случае начинаем с выражения для площади, где ab — площадь большого прямоугольника, а остальные слагаемые — площади меньших прямоугольников.

Раскрываем скобки в двух множителях c(d + d) и c(d + d + d):

S = ab — cd — c · 2d — c · 3d

Шаг 2: Приводим подобные слагаемые:

S = ab — cd — 2cd — 3cd

Шаг 3: Упрощаем выражение:

S = ab — 6cd

Таким образом, получаем окончательную формулу для площади S, где ab — площадь большого прямоугольника, а 6cd — общая площадь меньших прямоугольников.

Итоговые выражения:

• Для первой фигуры: S = ab — 2cd — c²
• Для второй фигуры: S = ab — 6cd