ГДЗ по Алгебра 7 Класс Номер 241 Дорофеев, Суворова — Подробные Ответы
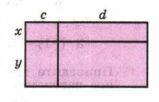
Составьте несколько различных выражений для вычисления площади прямоугольника (рис. 3.4) и запишите цепочку равенств.
1) \( (x + y)(c + d) \);
2) \( xc + xd + cy + dy \);
3) \( x(c + d) + y(c + d) \);
4) \( c(x + y) + d(x + y) \);
5) \( (x + y)(c + d) = xc + xd + cy + dy = x(c + d) + y(c + d) = \)
= \( c(x + y) + d(x + y) \).
1) \( (x + y)(c + d) \);
Это выражение представляет собой произведение двух скобок. Для его раскрытия используется распределительное свойство умножения. Раскрыв скобки, получаем:
\( (x + y)(c + d) = x(c + d) + y(c + d) \), где каждый член первой скобки умножается на каждую из составляющих второй скобки.
2) \( xc + xd + cy + dy \);
В этом выражении мы видим результат раскрытия скобок. Теперь каждая часть произведения стала отдельным слагаемым, и мы имеем сумму всех членов. Это результат применения распределительного свойства умножения.
3) \( x(c + d) + y(c + d) \);
Мы можем сгруппировать члены, объединяя \( x \) и \( y \) в одну часть, оставляя выражение в виде суммы произведений. Это выражение аналогично предыдущему, но записано немного по-другому, чтобы подчеркнуть структуру.
4) \( c(x + y) + d(x + y) \);
Здесь мы видим, что можно вынести общий множитель \( x + y \) из обоих членов. Это позволяет упростить выражение, получив:
\( c(x + y) + d(x + y) = (c + d)(x + y) \), где \( x + y \) является общим множителем, который сокращает выражение.
5) \( (x + y)(c + d) = xc + xd + cy + dy = x(c + d) + y(c + d) = \)
В этом шаге мы показали, что раскрытие скобок и перемещение множителей по-разному записывают одно и то же выражение. Все этапы эквивалентны, и результат остаётся одинаковым. Мы начинаем с первоначального выражения \( (x + y)(c + d) \), раскрываем скобки, получаем \( xc + xd + cy + dy \), затем группируем и перераспределяем множители:
\( x(c + d) + y(c + d) = c(x + y) + d(x + y) \), что и приводит нас к конечному виду:
\( c(x + y) + d(x + y) \), где мы видим, что результат остаётся неизменным при разных способах записи.
Ответ: Все эти способы демонстрируют эквивалентность разных методов раскрытия и группировки множителей, что позволяет записывать одно и то же выражение по-разному, но результат всегда остаётся одинаковым.