ГДЗ по Алгебра 7 Класс Номер 240 Дорофеев, Суворова — Подробные Ответы

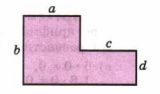
Найдите площадь фигуры (рис. 3.3) сначала вычитанием площадей, а потом сложением площадей и запишите соответствующее равенство.

Площадь фигуры вычитанием площадей: \( b(a + c) — c(b — d) \).

Площадь фигуры сложением площадей: \( ab + cd \).

Равенство:

\( b(a + c) — c(b — d) = ab + cd \)

\( ab + bc — bc = ab + cd \)

\( ab + cd = ab + cd \) — верно.

Задача: Рассмотрим выражения для вычисления площади фигуры.

Площадь фигуры вычитанием площадей: \( b(a + c) — c(b — d) \).

Здесь мы видим выражение для площади фигуры, которое вычисляется путём вычитания двух частей. Чтобы выполнить вычисление, необходимо раскрыть скобки и упростить выражение. Мы начинаем с того, что раскрываем скобки в обеих частях:

\( b(a + c) = ba + bc \),

\( c(b — d) = cb — cd \).

Теперь подставим эти выражения в исходную формулу:

\( b(a + c) — c(b — d) = (ba + bc) — (cb — cd) \).

Далее мы раскрываем скобки и приводим подобные члены:

\( ba + bc — cb + cd \).

Замечаем, что \( bc \) и \( cb \) одинаковы, но с противоположными знаками, поэтому они взаимно уничтожаются. Оставшиеся члены:

\( ba + cd \),

что даёт нам итоговое выражение для площади фигуры:

\( ab + cd \),

что и является результатом вычисления.

Площадь фигуры сложением площадей: \( ab + cd \).

Второй способ вычисления площади заключается в сложении двух площадей \( ab \) и \( cd \), где \( a \), \( b \), \( c \) и \( d \) — это стороны соответствующих частей фигуры. Это выражение даёт ту же самую площадь, что и при вычислении вычитанием.

Равенство:

Теперь, когда мы выполнили обе операции, мы можем показать, что результаты совпадают:

\( b(a + c) — c(b — d) = ab + cd. \)

Далее раскрываем скобки и приводим подобные члены:

\( ab + bc — bc = ab + cd \),

где \( bc — bc = 0 \), и остаётся:

\( ab + cd = ab + cd \),

что верно и подтверждает равенство.

Ответ: Оба способа дают одинаковый результат, и равенство справедливо.