ГДЗ по Алгебра 7 Класс Номер 231 Дорофеев, Суворова — Подробные Ответы

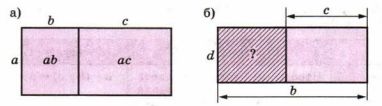
Рассмотрите рисунок 3.1, а. Для вычисления площади прямоугольника, изображённого на этом рисунке, можно составить выражение a(b + с) или выражение ab + ac. Числовое значение будет одно и то же: a(b + с) = ab + ас.
Составьте два разных выражения для вычисления площади заштрихованной части прямоугольника на рисунке 3.1,б и запишите соответствующее равенство.

а) \( a(b + c) = ab + ac \).

б) \( d(b — c) = db — dc \).

Задача:

а) \( a(b + c) = ab + ac \)

В данном примере используется распределительное свойство умножения, которое гласит, что при умножении числа на сумму двух других чисел, результат будет равен сумме произведений этого числа на каждое из чисел. То есть:

Если \( a \) умножается на сумму \( b + c \), то это равно:

\( a(b + c) = ab + ac \).

Этот закон позволяет упростить выражения с умножением на скобки и легко разложить их на более простые компоненты.

б) \( d(b — c) = db — dc \)

Здесь мы используем распределительное свойство умножения относительно разности. Это свойство аналогично предыдущему, но применяется к разности. Оно утверждает, что при умножении числа на разность двух других чисел, результат будет равен разности произведений этого числа на каждое из чисел:

\( d(b — c) = db — dc \).

Это свойство полезно, когда нужно упростить выражения, содержащие разности внутри скобок.

Ответ: Обе формулы иллюстрируют распределительные свойства для умножения относительно сложения и вычитания, которые помогают упростить алгебраические выражения.