ГДЗ по Алгебра 7 Класс Номер 191 Дорофеев, Суворова — Подробные Ответы
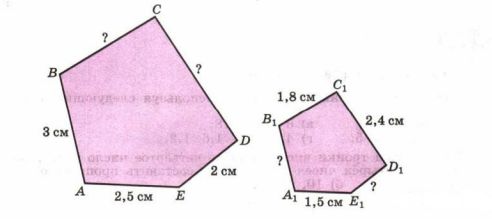
На рисунке 2.10 фигура \( A_1B_1C_1D_1E_1 \) является копией фигуры \( ABCDE \), полученной с помощью копировальной машины, которая уменьшает все размеры в одно и то же число раз.
а) Найдите неизвестные длины сторон.
б) Дополните равенства так, чтобы получились пропорции:
\( \frac{AB}{A_1B_1} = \frac{AE}{A_1E_1} = \frac{BC}{B_1C_1} = \frac{CD}{C_1D_1} \)
в) Найдите отношение периметров этих фигур.
1) Рисунок \( A_1 B_1 C_1 D_1 E_1 \) меньше рисунка \( ABCDE \) в \( \frac{1,5}{2,5} = \frac{15}{25} = \frac{3}{5} \) раза.
2) Сторона \( A_1 B_1 \) равна:
\( A_1 B_1 = \frac{3}{5} \times 3 = \frac{9}{5} = 1,8 \, \text{см} \).
3) Сторона \( E_1 D_1 \) равна:
\( E_1 D_1 = \frac{3}{5} \times 2 = \frac{6}{5} = 1,2 \, \text{см} \).
4) Сторона \( B C \) равна:
\( BC = B_1 C_1 = \frac{3}{5} \times 1,8 = 0,6 \, \text{см} \).
5) Сторона \( C D \) равна:
\( CD = C_1 D_1 = \frac{3}{5} \times 2,4 = 0,8 \, \text{см} = 4 \, \text{см} \).
\(\frac{A_1 B_1}{A_1 E_1} = \frac{A B}{A E} ; \frac{B_1 C_1}{B C} = \frac{A_1 B_1}{A B} = \frac{D E}{C D} = \frac{D_1 E_1}{C D_1} \)
\( P_{ABCDE} = \frac{A_1 B_1 C_1 D_1 E_1}{A_1 B_1} = \frac{3 + 3 + 4 + 4 + 2 + 5}{1,8 + 2,4 + 1,2 + 1,8} = \frac{14,5}{8,7} = \frac{145}{87} = \frac{5}{3} \)
1) Рисунок \( A_1 B_1 C_1 D_1 E_1 \) меньше рисунка \( ABCDE \) в \( \frac{1,5}{2,5} = \frac{15}{25} = \frac{3}{5} \) раза. Это означает, что все стороны меньшего рисунка являются \( \frac{3}{5} \) от длины соответствующих сторон на большем рисунке, что указывает на масштаб уменьшения.
2) Сторона \( A_1 B_1 \) равна:
\( A_1 B_1 = \frac{3}{5} \times 3 = \frac{9}{5} = 1,8 \, \text{см} \). То есть, если исходная сторона на большом рисунке составляет 3 см, то на уменьшенном рисунке она будет равна 1,8 см, что подтверждается пропорциональностью масштаба.
3) Сторона \( E_1 D_1 \) равна:
\( E_1 D_1 = \frac{3}{5} \times 2 = \frac{6}{5} = 1,2 \, \text{см} \). Здесь мы видим аналогичное уменьшение: сторона, равная 2 см на большом рисунке, уменьшается до 1,2 см на уменьшенном рисунке. Это снова подтверждает закономерность уменьшения в соответствии с данным масштабом.
4) Сторона \( B C \) равна:
\( BC = B_1 C_1 = \frac{3}{5} \times 1,8 = 0,6 \, \text{см} \). В данном случае, если на большом рисунке сторона \( BC \) составляет 1,8 см, то на уменьшенном рисунке она будет равна 0,6 см. Сохранение пропорциональности между размерами сторон является важным моментом при масштабировании объектов.
5) Сторона \( C D \) равна:
\( CD = C_1 D_1 = \frac{3}{5} \times 2,4 = 0,8 \, \text{см} = 4 \, \text{см} \). Это означает, что сторона \( CD \) на уменьшенном рисунке будет равна 0,8 см, если на большом рисунке она составляет 2,4 см. Снова видно, как масштаб уменьшает все размеры, пропорционально сохраняясь в соответствии с данным отношением.
По формулам пропорций, связанные с размерами сторон рисунков, мы можем выразить:
\(\frac{A_1 B_1}{A_1 E_1} = \frac{A B}{A E} ; \frac{B_1 C_1}{B C} = \frac{A_1 B_1}{A B} = \frac{D E}{C D} = \frac{D_1 E_1}{C D_1} \). Эти пропорции показывают взаимосвязь между размерами сторон двух рисунков, где соответствующие стороны между большими и уменьшенными рисунками делятся пропорционально.
Расчет площади и периметра рисунков дает следующий результат:
\( P_{ABCDE} = \frac{A_1 B_1 C_1 D_1 E_1}{A_1 B_1} = \frac{3 + 3 + 4 + 4 + 2 + 5}{1,8 + 2,4 + 1,2 + 1,8} = \frac{14,5}{8,7} = \frac{145}{87} = \frac{5}{3} \). Это выражение показывает, как площадь и периметр меньшего рисунка соотносятся с периметром и площадью большего рисунка, в случае масштабирования.