ГДЗ по Алгебра 7 Класс Номер 149 Дорофеев, Суворова — Подробные Ответы
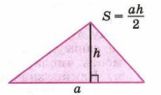
а) Из формулы площади треугольника \( S = \frac{ah}{2} \) (рис. 2.6) выразите \( h \) и \( a \):
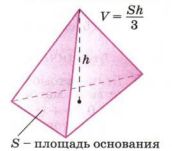
б) Из формулы объема пирамиды \( V = \frac{Sh}{3} \) (рис. 2.7) выразите \( h \) и \( S \):
а) \( S = \frac{ah}{2} \), \( 2S = ah \)
\( h = \frac{2S}{a} \), \( a = \frac{2S}{h} \)
б) \( V = \frac{Sh}{3} \), \( 3V = Sh \)
\( h = \frac{3V}{S} \), \( S = \frac{3V}{h} \)
а) Первая формула для площади треугольника:
Площадь треугольника вычисляется по формуле \( S = \frac{ah}{2} \), где:
\( S \) — площадь треугольника,
\( a \) — основание треугольника,
\( h \) — высота треугольника.
Если нам нужно выразить высоту \( h \) через площадь \( S \) и основание \( a \), то мы можем преобразовать формулу следующим образом:
Умножим обе части формулы на 2 и разделим на \( a \):
\( h = \frac{2S}{a} \).
Теперь, чтобы выразить основание \( a \), умножим обе части формулы на 2 и разделим на \( h \):
\( a = \frac{2S}{h} \).
б) Формула для объема пирамиды:
Объем пирамиды можно вычислить по формуле \( V = \frac{Sh}{3} \), где:
\( V \) — объем пирамиды,
\( S \) — площадь основания пирамиды,
\( h \) — высота пирамиды.
Чтобы выразить высоту \( h \) через объем \( V \) и площадь основания \( S \), умножим обе части формулы на 3 и разделим на \( S \):
\( h = \frac{3V}{S} \).
Теперь, чтобы выразить площадь основания \( S \), разделим обе части формулы на \( h \) и умножим на 3:
\( S = \frac{3V}{h} \).