ГДЗ по Алгебра 7 Класс Номер 144 Дорофеев, Суворова — Подробные Ответы
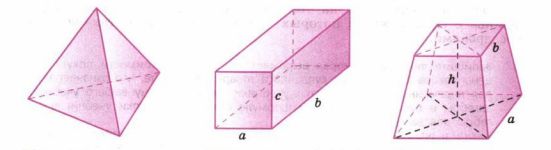
а) Объём тетраэдра — треугольной пирамиды, все рёбра которой равны (рис. 2.1), можно вычислить по приближённой формуле V = 7a3/60, где a — длина ребра. Найдите объём тетраэдра, если а = 6 см; а = 12 см.
б) Площадь поверхности прямоугольного параллелепипеда (рис. 2.2) вычисляется по формуле S = 2(ab + ас + bс), где а, b и с — измерения параллелепипеда. Найдите площадь поверхности, если а = 5 см, b = 7 см, с = 9 см.
в) Объём усечённой пирамиды с квадратными основаниями (рис. 2.3) вычисляется по формуле V =h/3*(a2 + b2 + ab), где h — высота усечённой пирамиды. Найдите объём, если h = 15 см, a = 20 см, b = 10 см.
а) \( V \approx \frac{7a^3}{60} \)
при \( a = 6 \, \text{см} \):
\( V \approx \frac{7 \cdot 6^3}{60} = \frac{7 \cdot 216}{60} = \frac{252}{10} = 25,2 \, \text{см}^3 \).
при \( a = 12 \, \text{см} \):
\( V \approx \frac{7 \cdot 12^3}{60} = \frac{7 \cdot 144 \cdot 12}{60} = \frac{7 \cdot 144 \cdot 2}{10} = \frac{2016}{10} = 201,6 \, \text{см}^3 \).
Ответ: \( 25,2 \, \text{см}^3 \); \( 201,6 \, \text{см}^3 \).
б) \( S = 2(ab + ac + bc) \)
при \( a = 5 \, \text{см}, b = 7 \, \text{см}, c = 9 \, \text{см} \):
\( S = 2(5 \cdot 7 + 5 \cdot 9 + 7 \cdot 9) = 2 \cdot (35 + 45 + 63) = 2 \cdot 143 = 286 \, \text{см}^2 \).
Ответ: \( 286 \, \text{см}^2 \).
в) \( V = \frac{h}{3}(a^2 + b^2 + ab) \)
при \( h = 15 \, \text{см}, a = 20 \, \text{см}, b = 10 \, \text{см} \):
\( V = \frac{15}{3}(20^2 + 10^2 + 20 \cdot 10) = 5 \cdot (400 + 100 + 200) = 5 \cdot 700 = 3500 \, \text{см}^3 \).
Ответ: \( 3500 \, \text{см}^3 \).
а) \( V \approx \frac{7a^3}{60} \)
В этой задаче мы используем формулу для вычисления объема, в которой \(a\) — это длина стороны основания определенной фигуры, а \(V\) — объем. Мы подставим различные значения для переменной \(a\), чтобы найти объем.
При \( a = 6 \, \text{см} \):
Подставляем значение \( a = 6 \) в формулу объема:
\( V \approx \frac{7 \cdot 6^3}{60} = \frac{7 \cdot 216}{60} = \frac{1512}{60} = 25,2 \, \text{см}^3 \).
Итак, для \( a = 6 \, \text{см} \), объем составляет \( 25,2 \, \text{см}^3 \).
Теперь подставим значение \( a = 12 \, \text{см} \):
Подставляем значение \( a = 12 \) в ту же самую формулу для объема:
\( V \approx \frac{7 \cdot 12^3}{60} = \frac{7 \cdot 144 \cdot 12}{60} = \frac{7 \cdot 144 \cdot 2}{10} = \frac{2016}{10} = 201,6 \, \text{см}^3 \).
Итак, для \( a = 12 \, \text{см} \), объем составляет \( 201,6 \, \text{см}^3 \).
Ответ: \( 25,2 \, \text{см}^3 \) для \( a = 6 \, \text{см} \) и \( 201,6 \, \text{см}^3 \) для \( a = 12 \, \text{см} \).
б) \( S = 2(ab + ac + bc) \)
Здесь мы имеем задачу на вычисление площади, где \(a\), \(b\) и \(c\) — это стороны прямоугольного параллелепипеда, и нужно вычислить площадь его поверхности. Для этого используется формула:
\( S = 2(ab + ac + bc) \), где \(ab\), \(ac\), и \(bc\) — это площади сторон, и мы удваиваем сумму этих площадей.
При \( a = 5 \, \text{см}, b = 7 \, \text{см}, c = 9 \, \text{см} \):
Подставляем данные значения в формулу для площади:
\( S = 2(5 \cdot 7 + 5 \cdot 9 + 7 \cdot 9) = 2 \cdot (35 + 45 + 63) = 2 \cdot 143 = 286 \, \text{см}^2 \).
Ответ: \( 286 \, \text{см}^2 \) для данных значений сторон.
в) \( V = \frac{h}{3}(a^2 + b^2 + ab) \)
В этой задаче нужно вычислить объем усеченной пирамиды с основанием, имеющим форму прямоугольного треугольника. Формула для объема в данном случае выглядит так:
\( V = \frac{h}{3}(a^2 + b^2 + ab) \), где \(h\) — высота пирамиды, \(a\) и \(b\) — длины сторон основания.
При \( h = 15 \, \text{см}, a = 20 \, \text{см}, b = 10 \, \text{см} \):
Подставляем все данные в формулу для объема:
\( V = \frac{15}{3}(20^2 + 10^2 + 20 \cdot 10) = 5 \cdot (400 + 100 + 200) = 5 \cdot 700 = 3500 \, \text{см}^3 \).
Ответ: \( 3500 \, \text{см}^3 \) для заданных значений.