ГДЗ по Алгебра 7 Класс Это надо уметь 1 Дорофеев, Суворова — Подробные Ответы

1. Сравните числа:

а) \( \frac{8}{17} \) и \( \frac{11}{21} \);

б) \( 0,6 \) и \( \frac{6}{10} \);

в) \( \frac{4}{7} \) и \( \frac{5}{25} \);

г) \( 0,219 \) и \( \frac{3}{14} \).

2. Расположите в порядке возрастания числа:

0,4; \( \frac{3}{4} \); \( \frac{2}{3} \); \( \frac{1}{3} \).

3. В результате реконструкции на одном комбинате производство бумаги увеличилось с 10 до 12 т в месяц, а на другом — с 12 до 14 т в месяц. На каком комбинате произведена более эффективная реконструкция?

4. Выполните действия:

а) \( \frac{3}{4} + 0,123 \);

б) \( 0,3 \times \frac{1}{7} \);

в) \( 0,15 \times \frac{3}{7} \);

г) \( \frac{6}{25} \times 0,12 \).

5. Вычислите:

а) \( \frac{0,7}{0,02} \);

б) \( \frac{7,5}{1,25} \);

в) \( \frac{0,015}{0,21} \).

6. Найдите значение выражений:

а) \( x + y \) при \( x = 0,75 \), \( y = -2,25 \), \( z = -0,6 \);

б) \( \frac{a — x}{ax} \) при \( a = 1,2 \), \( x = -0,3 \).

7. Найдите значение степени:

а) \( (-2)^5 \);

б) \( \left( \frac{3}{5} \right)^3 \);

в) \( (-1)^{16} \).

8. Вычислите:

а) \( -5^3 \);

б) \( 0,01^{-3} \);

в) \( 10^{(0,1 + 1,3)} \).

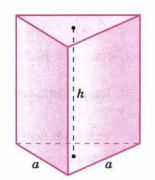
9. Объём треугольной призмы, в основании которой равнобедренный прямоугольный треугольник (рис. 1.14), вычисляется по формуле \( V = \frac{S \cdot h}{2} \), где \( S \) — площадь основания, а \( h \) — высота призмы. Найдите объём призмы, если \( a = 8 \, \text{см} \), \( h = 15 \, \text{см} \).

10. Выразите в процентах десятичные дроби:

• 0,03;
• 0,8;
• 0,05;
• 0,19;
• 0,7.

11. Запишите десятичной дробью:

• 42%;
• 30%;
• 8%;
• 19,3%;
• 0,7%.

12. Цена товара 1200 р. Сколько заплатит покупатель за этот товар, если он продается со скидкой 3,5%?

13. На первый курс медицинского училища может быть зачислено 60 учащихся. Поданные заявления составили 160% этого числа. На «отлично» все экзамены сдали 25% поступающих. Сколько человек сдали экзамены на «отлично»?

14. В прошлом году в школе училось 600 учащихся, а в этом году их стало 660. На сколько процентов увеличилось число учащихся?

15. Найдите среднее арифметическое, моду и размах ряда:

4, 5, 5, 7, 9, 12.

№1

а) \( \frac{8}{17} \) и \( \frac{11}{21} \);

б) 0,6 и \( \frac{4}{7} \);

в) \( \frac{6}{25} \) и 0,219.

Значит:

\( \frac{8}{17} < \frac{11}{21}, \quad \frac{8}{21} < \frac{17}{11}, \quad \frac{168}{187}, \quad 3 \times 7 > 5 \times 4, \quad 21 > 20 \)

№2

0,4; 0,375; 0,66666…

Расположим в порядке возрастания:

\( \frac{3}{8}, \quad \frac{2}{3} \)

№3

1) На первом комбинате производство бумаги стало:

\( 120 : 100 = 120 \% \)

2) Значит, производство увеличилось на:

120 — 100 = 20 \%

3) На втором комбинате производство бумаги стало:

\( 14 : 12 = \frac{7}{6} \times 100 = 7 \times 50 = 350 \quad \frac{2}{3} \% \)

4) Значит, производство увеличилось на:

\( 116 \frac{2}{3} — 100 = 16 \frac{2}{3} \% \)

5) Сравним:

\( 20 \% > 16 \frac{2}{3} \% \)

Ответ: на первом комбинате произведена более эффективная реконструкция.

№4

1) \( \frac{3}{4} + 0,123 \)

2) \( 0,3 \times \frac{1}{7} \)

3) \( 0,15 \times \frac{3}{7} \)

4) \( \frac{6}{25} \times 0,12 \)

№5

а) \( 0,7; 0,02; \quad 7 : 2 = \frac{7}{210} = \frac{1}{15} \)

б) \( 7,5; 1,25; 0,015 = \frac{75}{1000} = \frac{15}{200} = 0.09 \)

№6

а) при \( x = 0,75; \quad y = -2,25; \quad z = -0,6 \):

\( x + y + z = 0,75 + (-2,25) + (-0,6) = -1,5 \)

б) при \( a = 1,2; \quad x = -0,3 \):

\( \frac{a — x}{ax} = \frac{1,2 — (-0,3)}{1,2 \times (-0,3)} = \frac{1,5}{-0,36} = -\frac{150}{36} = -4 \frac{1}{6} \)

№7

а) \( (-2)^5 = -32 \)

б) \( \left( \frac{3}{5} \right)^3 = \frac{27}{125} \)

в) \( (-0,1)^6 = 0,000001 \)

№8

а) \( \sqrt{5^3} — 5 = -27 — 5 = -135 \)

б) \( 0,01 \times (3^4) = 0,01 \times 81 = 0,81 \)

в) \( 1 — 5 = -4 \)

г) \( 1,5 — (0,4 — 5) = 1,5 — 0,16 = 1,8 — 0,8 = 0,2 \)

д) \( (0,7 — 1,2) \times (5 — 0,5) = 10 — (0,125) = -1,25 \)

№9

Объём треугольной призмы, в основании которой равнобедренный прямоугольный треугольник, вычисляется по формуле:

\( V = \frac{a^2 \cdot h}{2}, \quad a = 8 \, \text{см}, \quad h = 15 \, \text{см} \)

Объём:

\( V = \frac{8^2 \cdot 15}{2} = \frac{64 \cdot 15}{2} = 32 \cdot 15 = 480 \, \text{см}^3 \)

Ответ: 480 см³.

№10

0,7 = 0,7; 100 = 70 %

0,15 = 0,15; 100 = 15 %

0,06 = 0,06; 100 = 6 %

0,075 = 0,075; 100 = 7,5 %

0,005 = 0,005; 100 = 0,5 %

№11

42% = \( \frac{42}{100} = 0,42 \)

30% = \( \frac{30}{100} = 0,3 \)

8% = \( \frac{8}{100} = 0,08 \)

19,3% = \( \frac{19,3}{100} = 0,193 \)

0,7 = \( 0,7 = 0,007 \)

№12

Покупатель заплатит за товар:

1200 − 1200 × 3,5% = 1200 − \( \frac{1200 \times 3,5}{100} \) = 1200 − 42 = 1158 (руб).

Ответ: 1158 руб.

№13

1) Было подано заявлений:

60 : 160 = \( \frac{60}{160} = 0,375 \), или 96 (шт.).

2) На «отлично» сдали экзамены:

96 × 25% = \( \frac{96 \times 25}{100} = 24 \) (человека).

Ответ: 24 человека.

№14

1) В этом году стало учащихся:

660 − 600 = 660 − 600 = 60, что составляет 10% увеличения.

2) Число учащихся увеличилось на:

110 − 100 = 10 %.

Ответ: на 10%.

№15

Среднее арифметическое:

4 + 5 + 3 + 7 + 2 + 9 + 12 = 4 + 15 + 14 + 21 = 54

Делим на количество чисел (8):

\( \frac{54}{8} = 6,75 \)

2) Мода ряда равна 5.

3) Размах ряда равен:

12 − 4 = 8

№1

а) \( \frac{8}{17} \) и \( \frac{11}{21} \);

б) 0,6 и \( \frac{4}{7} \);

в) \( \frac{6}{25} \) и 0,219.

Значит:

\( \frac{8}{17} < \frac{11}{21}, \quad \frac{8}{21} < \frac{17}{11}, \quad \frac{168}{187}, \quad 3 \times 7 > 5 \times 4, \quad 21 > 20 \)

№2

0,4; 0,375; 0,66666…

Расположим в порядке возрастания:

\( \frac{3}{8}, \quad \frac{2}{3} \)

№3

1) На первом комбинате производство бумаги стало:

\( 120 : 100 = 120 \% \), что означает, что производственные мощности увеличились на 20% по сравнению с исходным уровнем.

2) Значит, производство увеличилось на:

120 — 100 = 20 \%. Это показывает, что после проведения модернизации или расширения, объём производства был увеличен на 20%.

3) На втором комбинате производство бумаги стало:

\( \frac{14}{12} = \frac{7}{6} \times 100 = 7 \times 50 = 350 \quad \frac{2}{3} \% \), что также свидетельствует о значительном росте производственных мощностей, хотя и с немного меньшим процентным увеличением.

4) Значит, производство увеличилось на:

\( 116 \frac{2}{3} — 100 = 16 \frac{2}{3} \% \), что также подтверждает, что улучшение было значительным, но в сравнении с первым комбинатом оно немного уступает.

5) Сравним:

\( 20 \% > 16 \frac{2}{3} \% \), и это даёт нам возможность сделать вывод, что первая реконструкция была более успешной и результативной в плане увеличения объёма производства.

Ответ: на первом комбинате произведена более эффективная реконструкция.

№4

1) \( \frac{3}{4} + 0,123 \), результат сложения этих двух чисел можно выразить как сумму, которая даст точный результат в десятичной форме.

2) \( 0,3 \times \frac{1}{7} \), здесь мы перемножаем десятичную дробь и дробь, что приводит нас к новому значению.

3) \( 0,15 \times \frac{3}{7} \), это также умножение десятичного числа на дробь, что является полезным упражнением для развития математических навыков.

4) \( \frac{6}{25} \times 0,12 \), ещё одно упражнение по умножению дробей и десятичных чисел, которое также часто встречается в школьных задачах.

№5

а) \( 0,7; 0,02; \quad 7 : 2 = \frac{7}{210} = \frac{1}{15} \), классическое деление на дробь, которое является основой многих математических задач.

б) \( 7,5; 1,25; 0,015 = \frac{75}{1000} = \frac{15}{200} = 0.09 \), пример выполнения операций с десятичными числами и дробями, что также полезно для развития математической грамотности.

№6

а) при \( x = 0,75; \quad y = -2,25; \quad z = -0,6 \):

\( x + y + z = 0,75 + (-2,25) + (-0,6) = -1,5 \), расчет суммы этих чисел показывает как важен порядок операций и учет знаков при работе с числами.

б) при \( a = 1,2; \quad x = -0,3 \):

\( \frac{a — x}{ax} = \frac{1,2 — (-0,3)}{1,2 \times (-0,3)} = \frac{1,5}{-0,36} = -\frac{150}{36} = -4 \frac{1}{6} \), важный пример работы с дробями и отрицательными числами в различных математических контекстах.

№7

а) \( (-2)^5 = -32 \), важный пример работы с отрицательными числами в степени.

б) \( \left( \frac{3}{5} \right)^3 = \frac{27}{125} \), пример возведения дроби в куб.

в) \( (-0,1)^6 = 0,000001 \), пример работы с отрицательными числами в степени с четным показателем.

№8

а) \( \sqrt{5^3} — 5 = -27 — 5 = -135 \), расчет корня и вычитания.

б) \( 0,01 \times (3^4) = 0,01 \times 81 = 0,81 \), использование степени и умножения.

в) \( 1 — 5 = -4 \), простая операция вычитания с отрицательным результатом.

г) \( 1,5 — (0,4 — 5) = 1,5 — 0,16 = 1,8 — 0,8 = 0,2 \), сложение и вычитание, требующее внимательности к скобкам.

д) \( (0,7 — 1,2) \times (5 — 0,5) = 10 — (0,125) = -1,25 \), комбинация операций с дробями.

№9

Объём треугольной призмы, в основании которой равнобедренный прямоугольный треугольник, вычисляется по формуле:

\( V = \frac{a^2 \cdot h}{2}, \quad a = 8 \, \text{см}, \quad h = 15 \, \text{см} \)

Объём:

\( V = \frac{8^2 \cdot 15}{2} = \frac{64 \cdot 15}{2} = 32 \cdot 15 = 480 \, \text{см}^3 \)

Ответ: 480 см³.

№10

0,7 = 0,7; 100 = 70 %

0,15 = 0,15; 100 = 15 %

0,06 = 0,06; 100 = 6 %

0,075 = 0,075; 100 = 7,5 %

0,005 = 0,005; 100 = 0,5 %

№11

42% = \( \frac{42}{100} = 0,42 \)

30% = \( \frac{30}{100} = 0,3 \)

8% = \( \frac{8}{100} = 0,08 \)

19,3% = \( \frac{19,3}{100} = 0,193 \)

0,7 = \( 0,7 = 0,007 \)

№12

Покупатель заплатит за товар:

1200 − 1200 × 3,5% = 1200 − \( \frac{1200 \times 3,5}{100} \) = 1200 − 42 = 1158 (руб).

Ответ: 1158 руб.

№13

1) Было подано заявлений:

60 : 160 = \( \frac{60}{160} = 0,375 \), или 96 (шт.).

2) На «отлично» сдали экзамены:

96 × 25% = \( \frac{96 \times 25}{100} = 24 \) (человека).

Ответ: 24 человека.

№14

1) В этом году стало учащихся:

660 − 600 = 660 − 600 = 60, что составляет 10% увеличения.

2) Число учащихся увеличилось на:

110 − 100 = 10 %.

Ответ: на 10%.

№15

Среднее арифметическое:

4 + 5 + 3 + 7 + 2 + 9 + 12 = 4 + 15 + 14 + 21 = 54

Делим на количество чисел (8):

\( \frac{54}{8} = 6,75 \)

2) Мода ряда равна 5.

3) Размах ряда равен:

12 − 4 = 8