Учебник по математике для 6-го класса авторов Дорофеева и Шарыгина — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
Что выделяет этот учебник среди других:
- Понятное изложение материала. Каждая тема объясняется простым и доступным языком, что облегчает понимание даже сложных понятий.
- Большое количество примеров и задач. Учебник предлагает разнообразные упражнения — от простых до более сложных, что помогает закрепить пройденный материал.
- Интерактивный подход. В книге есть задания, которые побуждают учеников к самостоятельному поиску решений и развитию творческого мышления.
- Связь с реальной жизнью. Многие задачи связаны с практическими ситуациями, что делает математику более живой и понятной.
- Разнообразие форм подачи информации. Здесь используются таблицы, схемы, иллюстрации, что помогает лучше усваивать материал и удерживать внимание учащихся.
ГДЗ по Математике 6 Класс Номер 999 Дорофеев, Шарыгин — Подробные Ответы
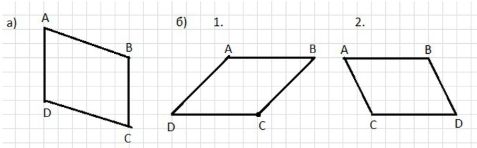
а) Начертите в тетради, используя свойства клетчатой бумаги, какойнибудь параллелограмм.
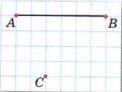
б) Точки A, B и C — вершины параллелограмма, АВ — его сторона (рис. 12.9). Постройте точку D — четвёртую вершину параллелограмма. Сколькими способами это можно сделать?
а) Начертите в тетради, используя свойства клетчатой бумаги, какой-нибудь параллелограмм.
Для того чтобы начертить параллелограмм на клетчатой бумаге, используйте свойства сетки. Начертите одну сторону параллелограмма (например, отрезок AB). Затем с помощью линейки и угольника постройте другие стороны параллелограмма, соблюдая параллельность противоположных сторон и равенство их длины. Чтобы избежать ошибок, можно использовать клетки на бумаге для точности, делая отрезки параллельными и равными.
б) Точки A, B и C — вершины параллелограмма, АВ — его сторона (рис. 12.9). Постройте точку D — четвёртую вершину параллелограмма. Сколькими способами это можно сделать?
Для того чтобы найти четвёртую вершину параллелограмма, необходимо помнить, что в параллелограмме противоположные стороны равны и параллельны. Итак, если у нас есть три вершины параллелограмма (A, B и C), то для построения точки D можно воспользоваться двумя способами:
- Способ 1: Использовать вектор AB (сторона параллелограмма) и провести отрезок, равный этому вектору, от точки C. Полученная точка будет вершиной D.
- Способ 2: Использовать вектор BC и провести отрезок, равный этому вектору, от точки A. Это также даст точку D.
Оба метода дадут одно и то же положение точки D, так как параллелограмм имеет симметричную структуру, и стороны всегда будут параллельны. Таким образом, точку D можно построить двумя способами.
