Учебник по математике для 6-го класса авторов Дорофеева и Шарыгина — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
Что выделяет этот учебник среди других:
- Понятное изложение материала. Каждая тема объясняется простым и доступным языком, что облегчает понимание даже сложных понятий.
- Большое количество примеров и задач. Учебник предлагает разнообразные упражнения — от простых до более сложных, что помогает закрепить пройденный материал.
- Интерактивный подход. В книге есть задания, которые побуждают учеников к самостоятельному поиску решений и развитию творческого мышления.
- Связь с реальной жизнью. Многие задачи связаны с практическими ситуациями, что делает математику более живой и понятной.
- Разнообразие форм подачи информации. Здесь используются таблицы, схемы, иллюстрации, что помогает лучше усваивать материал и удерживать внимание учащихся.
ГДЗ по Математике 6 Класс Номер 997 Дорофеев, Шарыгин — Подробные Ответы
Работаем с символами.
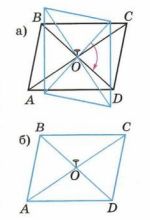
Воспользуйтесь результатами эксперимента с калькой (см. рис. 12.2) и допишите равенства: АВ = …, ВС = …, ОС = …, OD = …, угол A = …, угол B = …, треугольник АВО =…, треугольник АВС = … .
AB = CD; BC = AD; OC = OA; OD = OB;
∠A = ∠C; ∠B = ∠D;
△ABO = △DCO;
△ABC = △ADC.
Условия:
AB = CD; BC = AD; OC = OA; OD = OB;
∠A = ∠C; ∠B = ∠D;
△ABO = △DCO;
△ABC = △ADC.
Объяснение:
1. AB = CD, BC = AD, OC = OA, OD = OB; — Эти равенства говорят нам о том, что соответствующие стороны и отрезки, соединяющие точки на плоскости, равны между собой. Это может означать, что фигуры, которые мы рассматриваем, могут быть симметричными или геометрически связанными, например, о прямоугольниках, параллелограммах или треугольниках.
2. ∠A = ∠C, ∠B = ∠D; — Эти равенства углов означают, что углы при точках A и C, а также углы при точках B и D, равны. Это ещё раз указывает на симметрию в нашей геометрической фигуре, что важно для доказательства равенства треугольников.
3. △ABO = △DCO; — Эти треугольники равны по всем соответствующим сторонам и углам (по признаку равенства треугольников). Это можно доказать с помощью уже заданных равенств сторон и углов.
4. △ABC = △ADC; — Равенство этих треугольников также подтверждается тем, что у них равны соответствующие стороны и углы. Это может быть использовано для дальнейших доказательств или нахождения других свойств в фигуре.
