Учебник по математике для 6-го класса авторов Дорофеева и Шарыгина — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
Что выделяет этот учебник среди других:
- Понятное изложение материала. Каждая тема объясняется простым и доступным языком, что облегчает понимание даже сложных понятий.
- Большое количество примеров и задач. Учебник предлагает разнообразные упражнения — от простых до более сложных, что помогает закрепить пройденный материал.
- Интерактивный подход. В книге есть задания, которые побуждают учеников к самостоятельному поиску решений и развитию творческого мышления.
- Связь с реальной жизнью. Многие задачи связаны с практическими ситуациями, что делает математику более живой и понятной.
- Разнообразие форм подачи информации. Здесь используются таблицы, схемы, иллюстрации, что помогает лучше усваивать материал и удерживать внимание учащихся.
ГДЗ по Математике 6 Класс Номер 987 Дорофеев, Шарыгин — Подробные Ответы
Анализируем.
1) На координатной плоскости постройте данную точку; точку, симметричную ей относительно оси х, и запишите её координаты:
а) A(6; 2);
б) B(3; -1);
в) С(2; 4,5);
г) D(-3,5; -3,5).
Подметьте закономерность и ответьте на вопрос: как связаны между собой координаты у и координаты х точек, симметричных относительно оси х?
2) На координатной плоскости постройте данную точку; точку, симметричную ей относительно оси у, и запишите её координаты:
а) A(5; 1);
б) B(4; -2,5);
в) С(-3; 4);
г) D(-1,5; -6).
Подметьте закономерность и ответьте на вопрос: как связаны между собой координаты х и координаты у точек, симметричных относительно оси у?
3) Попробуйте, не выполняя построения, определить координаты точки, симметричной точке M(-5; 4):
а) относительно оси х;
б) относительно оси у.
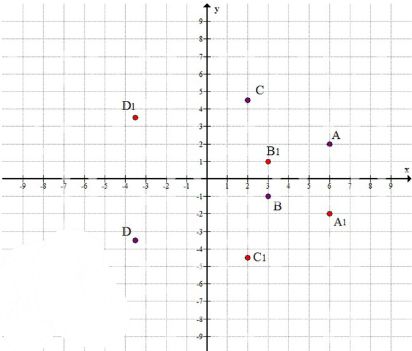
1) A (6; 2); B (-3; -1); C (2; 4.5); D (-3.5; -3.5);
A1 (6; -2); B1 (3; 1); C1 (2; -4.5); D1 (-3.5; 3.5).
Законечность следующая: координаты x совпадают, а координаты y — противоположные.
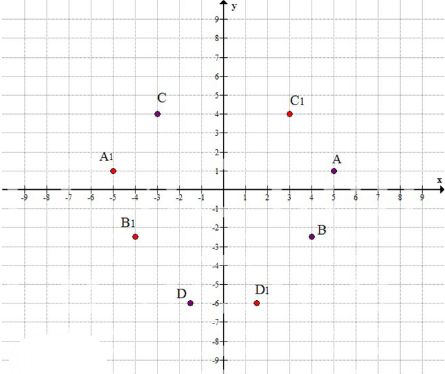
2) A (5; 1); B (4; -2.5); C (-3; 4); D (-1.5; -6);
A1 (-5; 1); B1 (-4; -2.5); C1 (3; 4); D1 (1.5; -6).
Законечность следующая: координаты y совпадают, а координаты x — противоположные.
3) M (-5; 4);
а) симметричная её точка относительно оси x: M1 (-5; -4);
б) симметричная её точка относительно оси y: M2 (5; 4).
1) Даны следующие точки:
- A (6; 2) — точка A расположена в I квадранте, так как её координаты положительные. Она находится в верхней правой части координатной плоскости.
- B (-3; -1) — точка B находится в III квадранте, так как обе её координаты отрицательные. Это указывает на её расположение в нижней левой части координатной плоскости.
- C (2; 4.5) — точка C расположена в I квадранте, так как обе её координаты положительные. Она находится выше точки A.
- D (-3.5; -3.5) — точка D также находится в III квадранте, так как обе её координаты отрицательные.
Для каждой из данных точек существует симметричные точки относительно оси X и оси Y. Законечность следующая: координаты X совпадают, а координаты Y — противоположные.
- A1 (6; -2) — точка симметрична точке A относительно оси X, так как координата Y меняет знак на противоположный.
- B1 (3; 1) — точка симметрична точке B относительно оси X.
- C1 (2; -4.5) — точка симметрична точке C относительно оси X.
- D1 (-3.5; 3.5) — точка симметрична точке D относительно оси X.
2) Даны следующие точки:
- A (5; 1) — точка A находится в I квадранте.
- B (4; -2.5) — точка B расположена в IV квадранте.
- C (-3; 4) — точка C расположена в II квадранте.
- D (-1.5; -6) — точка D расположена в III квадранте.
Законечность следующая: координаты Y совпадают, а координаты X — противоположные. Это означает, что все точки, симметричные относительно оси Y, имеют одинаковую Y-координату, а X-координаты противоположны.
- A1 (-5; 1) — точка симметрична точке A относительно оси Y.
- B1 (-4; -2.5) — точка симметрична точке B относительно оси Y.
- C1 (3; 4) — точка симметрична точке C относительно оси Y.
- D1 (1.5; -6) — точка симметрична точке D относительно оси Y.
3) Точка M (-5; 4).
- а) Симметричная точка относительно оси X: M1 (-5; -4). При симметрии относительно оси X координата X остаётся неизменной, а координата Y меняет знак на противоположный.
- б) Симметричная точка относительно оси Y: M2 (5; 4). При симметрии относительно оси Y координата Y остаётся неизменной, а координата X меняет знак на противоположный.
