ГДЗ по Математике 6 Класс Учебник 📕 Дорофеев, Шарыгин — Все Части

Математика

6 класс учебник Дорофеев

6 класс

Тип

ГДЗ, Решебник.

Авторы

Дорофеев Г.В., Шарыгин И.Ф., Суворова С.Б. и др.

Год

2010-2023.

Издательство

Просвещение.

Описание

Учебник по математике для 6-го класса авторов Дорофеева и Шарыгина — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.

Что выделяет этот учебник среди других:

Понятное изложение материала. Каждая тема объясняется простым и доступным языком, что облегчает понимание даже сложных понятий.
Большое количество примеров и задач. Учебник предлагает разнообразные упражнения — от простых до более сложных, что помогает закрепить пройденный материал.
Интерактивный подход. В книге есть задания, которые побуждают учеников к самостоятельному поиску решений и развитию творческого мышления.
Связь с реальной жизнью. Многие задачи связаны с практическими ситуациями, что делает математику более живой и понятной.
Разнообразие форм подачи информации. Здесь используются таблицы, схемы, иллюстрации, что помогает лучше усваивать материал и удерживать внимание учащихся.

ГДЗ по Математике 6 Класс Номер 985 Дорофеев, Шарыгин — Подробные Ответы

Задача

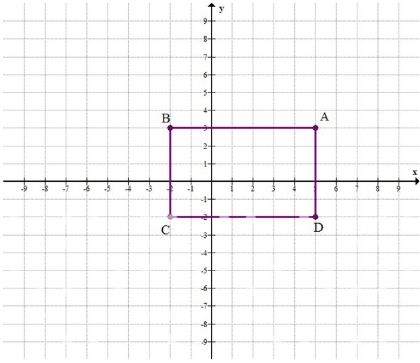
а) На координатной плоскости постройте прямоугольник ABCD по координатам его вершин: A(5; 3), В(-2; 3), С(-2; -2), D(5; -2). Вычислите периметр и площадь прямоугольника ABCD.
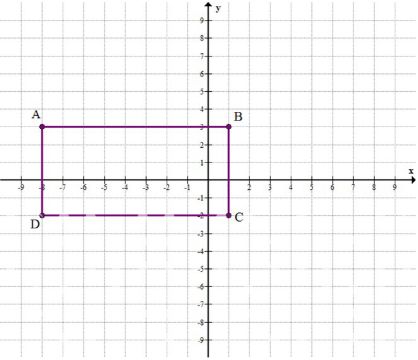
б) На координатной плоскости отметьте точки A(-8; 3), В(1; 3), С(1; -2). Постройте четвёртую точку D так, чтобы получился прямоугольник ABCD. Вычислите его периметр и площадь.

Краткий ответ:

а) Точки A (5; 3), B (-2; 3), C (-2; -2), D (5; -2).

Длины сторон:

AB = CD = 7 ед.;
BC = AD = 5 ед.

Периметр равен: 2(7 + 5) = 2 * 12 = 24 ед.

Площадь равна: 7 * 5 = 35 кв. ед.

Ответ: 24 ед.; 35 кв. ед.

б) Точки A (-8; 3), B (1; 3), C (1; -2), D (-8; -2).

Длины сторон:

AB = CD = 9 ед.;
BC = AD = 5 ед.

Периметр равен: 2(9 + 5) = 2 * 14 = 28 ед.

Площадь равна: 9 * 5 = 45 кв. ед.

Ответ: 28 ед.; 45 кв. ед.

Подробный ответ:

а) Треугольник с вершинами A (5; 3), B (-2; 3), C (-2; -2), D (5; -2).

Длины сторон этого треугольника:

AB = CD = 7 ед. — отрезок AB соединяет точки A и B, а отрезок CD соединяет точки C и D. Для вычисления длины отрезков используется формула расстояния между двумя точками на плоскости:
d = √((x2 — x1)² + (y2 — y1)²), где (x1, y1) и (x2, y2) — координаты двух точек.
BC = AD = 5 ед. — отрезок BC соединяет точки B и C, а отрезок AD соединяет точки A и D. Для этих отрезков также используется формула расстояния.

Периметр треугольника равен сумме длин его сторон:

2(7 + 5) = 2 * 12 = 24 ед. — это длина всего периметра, полученная путем сложения всех сторон треугольника.

Площадь треугольника вычисляется по формуле для площади прямоугольного треугольника, где одна сторона является основанием, а другая — высотой. Площадь равна:

7 * 5 = 35 кв. ед. — площадь треугольника определяется умножением основания на высоту.

Ответ: Периметр = 24 ед.; Площадь = 35 кв. ед.

б) Четырехугольник с вершинами A (-8; 3), B (1; 3), C (1; -2), D (-8; -2).

Длины сторон этого четырехугольника:

AB = CD = 9 ед. — отрезок AB соединяет точки A и B, а отрезок CD соединяет точки C и D. Эти отрезки имеют одинаковую длину, что подтверждается расчетами.
BC = AD = 5 ед. — отрезок BC соединяет точки B и C, а отрезок AD соединяет точки A и D. Эти отрезки также имеют одинаковую длину.

Периметр четырехугольника равен сумме длин всех его сторон: