Учебник по математике для 6-го класса авторов Дорофеева и Шарыгина — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
Что выделяет этот учебник среди других:
- Понятное изложение материала. Каждая тема объясняется простым и доступным языком, что облегчает понимание даже сложных понятий.
- Большое количество примеров и задач. Учебник предлагает разнообразные упражнения — от простых до более сложных, что помогает закрепить пройденный материал.
- Интерактивный подход. В книге есть задания, которые побуждают учеников к самостоятельному поиску решений и развитию творческого мышления.
- Связь с реальной жизнью. Многие задачи связаны с практическими ситуациями, что делает математику более живой и понятной.
- Разнообразие форм подачи информации. Здесь используются таблицы, схемы, иллюстрации, что помогает лучше усваивать материал и удерживать внимание учащихся.
ГДЗ по Математике 6 Класс Номер 984 Дорофеев, Шарыгин — Подробные Ответы
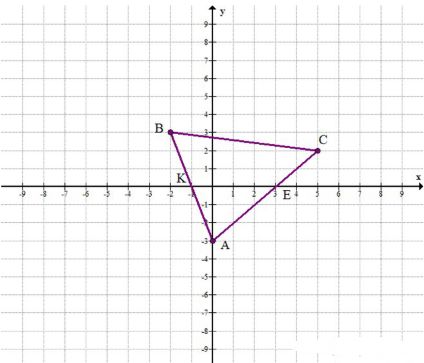
а) Постройте треугольник, если известны координаты его вершин: А(0; -3), В(-2; 3), С(5; 2). Укажите координаты точек, в которых стороны треугольника пересекают ось х.
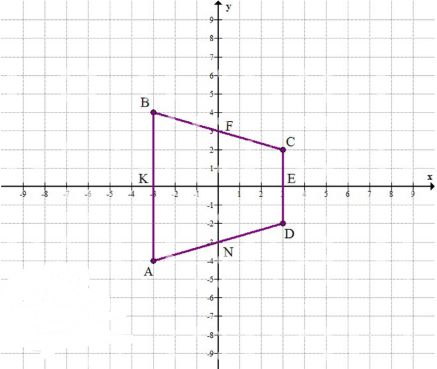
б) Постройте четырёхугольник ABCD, если его вершины имеют координаты: A(-3; -4), B(-3; 4), С(3; 2), D(3; -2). Укажите координаты точек, в которых стороны четырёхугольника пересекают оси координат.
а) A (0; -3); B (-2; 3); C (5; 2); E (3; 0) и K (-1; 0) — точки пересечения с осью X.
б) A (-3; -4); B (-3; 4); C (3; 2); D (3; -2); K (-3; 0); E (3; 0); F (0; 3); N (0; -3) — точки пересечения с осями координат.
а) A (0; -3), B (-2; 3), C (5; 2), E (3; 0), и K (-1; 0) — точки пересечения с осью X.
Для каждой из данных точек (A, B, C, E, K) можно провести прямую, соединяющую две точки, и найти точку пересечения этой прямой с осью X.
- A (0; -3) — точка A находится на оси Y, так как её координата по оси X равна 0, и она пересекает ось X в точке (0, 0).
- B (-2; 3) — точка B находится в II квадранте, так как X отрицательный, а Y положительный, и пересекает ось X на оси X в точке, которую можно вычислить по уравнению прямой, соединяющей точки A и B.
- C (5; 2) — точка C находится в I квадранте и пересекает ось X на основе уравнения прямой, соединяющей эту точку с B.
- E (3; 0) — точка E лежит на оси X, так как её Y-координата равна 0, и она пересекает ось X в точке (3, 0).
- K (-1; 0) — точка K лежит на оси X, так как её Y-координата равна 0, и пересекает ось X в точке (-1, 0).
б) A (-3; -4), B (-3; 4), C (3; 2), D (3; -2), K (-3; 0), E (3; 0), F (0; 3), N (0; -3) — точки пересечения с осями координат.
Для данного четырёхугольника, состоящего из точек A, B, C, D, K, E, F, N, можно найти точки пересечения с осями координат:
- A (-3; -4) — точка A находится в III квадранте, так как обе координаты отрицательные, и пересекает ось X на основе уравнения прямой.
- B (-3; 4) — точка B находится во II квадранте, и пересекает ось X на основе уравнения прямой.
- C (3; 2) — точка C находится в I квадранте, и пересекает ось X.
- D (3; -2) — точка D находится в IV квадранте, и пересекает ось X на основе уравнения прямой.
- K (-3; 0) — точка K лежит на оси X и пересекает её в точке (-3, 0).
- E (3; 0) — точка E лежит на оси X и пересекает её в точке (3, 0).
- F (0; 3) — точка F лежит на оси Y, и её пересечение с осью X можно определить по уравнению прямой, проходящей через эту точку и другие.
- N (0; -3) — точка N лежит на оси Y, и пересекает ось X по аналогичной логике, используя уравнение прямой.
