ГДЗ по Математике 6 Класс Номер 983 Дорофеев, Шарыгин — Подробные Ответы

Постройте отрезок АВ по координатам его концов и найдите координаты точки, в которой он пересекает ось х:
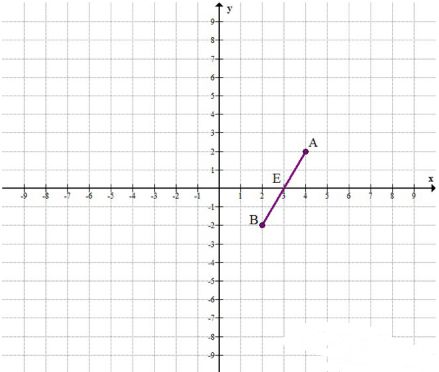
а) A(4; 2), B(2; -2);
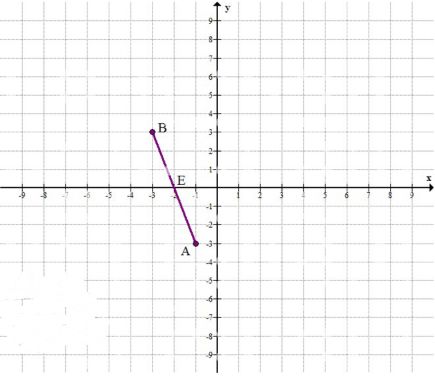
б) A(-1; -3), B(-3; 3).

а) Для отрезка A(4; 2), B(2; -2) точка пересечения с осью X имеет координату (3, 0).

б) Для отрезка A(-1; -3), B(-3; 3) точка пересечения с осью X имеет координату (-2, 0).

а) Для нахождения уравнения прямой, проходящей через точки \(A(4; 2)\) и \(B(2; -2)\), сначала необходимо определить угловой коэффициент \(k\). Угловой коэффициент показывает, насколько сильно изменяется значение \(y\) при изменении \(x\). Формула для вычисления углового коэффициента между двумя точками такова: \(k = \frac{y_2 — y_1}{x_2 — x_1}\), где \((x_1, y_1)\) и \((x_2, y_2)\) — координаты двух точек. Подставляя значения, получаем \(k = \frac{-2 — 2}{2 — 4} = \frac{-4}{-2} = 2\). Это значит, что при увеличении \(x\) на 1, \(y\) увеличивается на 2.

Далее, зная \(k\), можно записать уравнение прямой в виде \(y = kx + b\), где \(b\) — это свободный член, отвечающий за смещение прямой по оси \(y\). Чтобы найти \(b\), подставим координаты одной из точек, например, точки \(A\): \(2 = 2 \cdot 4 + b\). Решая уравнение, получаем \(b = 2 — 8 = -6\). Таким образом, уравнение прямой примет вид \(y = 2x — 6\).

Чтобы найти точку пересечения этой прямой с осью \(x\), нужно понять, что на оси \(x\) значение \(y\) всегда равно нулю. Подставим \(y = 0\) в уравнение: \(0 = 2x — 6\). Решая это уравнение, получаем \(x = 3\). Следовательно, точка пересечения с осью \(x\) — это \(E(3; 0)\).

б) Аналогично, для точек \(A(-1; -3)\) и \(B(-3; 3)\) сначала вычислим угловой коэффициент по формуле \(k = \frac{y_2 — y_1}{x_2 — x_1}\). Подставим значения: \(k = \frac{3 — (-3)}{-3 — (-1)} = \frac{6}{-2} = -3\). Отрицательное значение коэффициента говорит о том, что прямая направлена вниз при движении слева направо.

Затем запишем уравнение прямой \(y = kx + b\) и подставим координаты точки \(A\): \(-3 = -3 \cdot (-1) + b\). Решая, получаем \(b = -3 — 3 = -6\). Значит уравнение прямой: \(y = -3x — 6\).

Для нахождения точки пересечения с осью \(x\) подставим \(y = 0\): \(0 = -3x — 6\). Решая уравнение, получаем \(x = -2\). Значит точка пересечения с осью \(x\) — \(E(-2; 0)\).