Учебник по математике для 6-го класса авторов Дорофеева и Шарыгина — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
ГДЗ по Математике 6 Класс Номер 963 Дорофеев, Шарыгин — Подробные Ответы
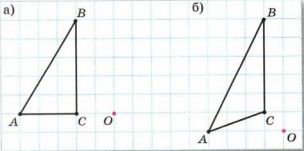
Скопируйте рисунок в тетрадь и постройте фигуру, симметричную данной относительно точки О (рис. 11.17, а, б).
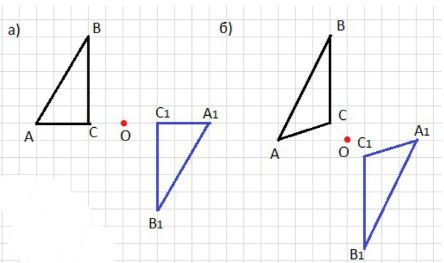
Построение симметричной фигуры относительно точки O:
1. Построение симметричной фигуры относительно точки O (для рис. 11.17, а):
- Нарисуйте треугольник ABC, как показано на рисунке а.
- Точка O — это точка симметрии.
- Для каждой вершины треугольника, например, для точки A, постройте прямую, проходящую через точку O и перпендикулярную к стороне, которая соединяет вершину с точкой O.
- Измерьте расстояние от точки O до каждой вершины треугольника и отметьте точку симметрии, которая будет на том же расстоянии, но на противоположной стороне.
- Повторите это для всех вершин, и соедините новые точки для получения симметричного треугольника.
2. Построение симметричной фигуры относительно точки O (для рис. 11.17, б):
- Повторите аналогичные шаги для второй фигуры.
- Точка O также будет центром симметрии.
- Используйте те же методы для построения симметричных точек относительно O, чтобы создать зеркальное изображение второй фигуры.
Эти шаги помогут вам построить симметричные фигуры на основе оригинала относительно точки O.
