
Учебник по математике для 6-го класса авторов Дорофеева и Шарыгина — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
ГДЗ по Математике 6 Класс Номер 957 Дорофеев, Шарыгин — Подробные Ответы
Исследуем.
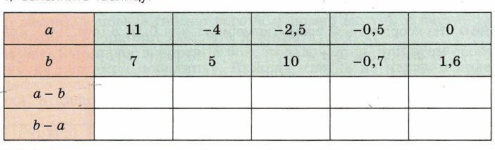
1) Заполните таблицу.
Какую закономерность вы заметили?
2) Используя подмеченную закономерность, найдите значение выражения:
а) \(\frac{3 — 5}{5 — 3}\)
б) \(\frac{0,4 — 0,6}{0,6 — 0,4}\)
в) \(\frac{\frac{1}{2} — \frac{1}{3}}{\frac{3}{2} — 1}\)
г) \(\frac{1 — 0,72}{0,72 — 1}\)
д) \(\frac{3 — 0,2}{0,2 — 3}\)
е) \(\frac{-(25 — 1)}{1 — 2,5}\)
1) Заполняем таблицу, вычисляя \(a-b\) и \(b-a\):
| \(a\) | 11 | -4 | -2,5 | -0,5 | 0 |
| \(b\) | 7 | 5 | 10 | -0,7 | 1,6 |
| \(a-b\) | 11-7=4 | -4-5=-9 | -2,5-10=-12,5 | -0,5-(-0,7)=0,2 | 0-1,6=-1,6 |
| \(b-a\) | 7-11=-4 | 5-(-4)=9 | 10-(-2,5)=12,5 | -0,7-(-0,5)=-0,2 | 1,6-0=1,6 |
Замечаем, что \(b-a = -(a-b)\).
2) Используя закономерность, вычисляем:
а) \(\frac{3-5}{5-3} = \frac{-2}{2} = -1\)
б) \(\frac{0,4-0,6}{0,6-0,4} = \frac{-0,2}{0,2} = -1\)
в) \(\frac{\frac{1}{3}-\frac{1}{2}}{\frac{1}{2}-\frac{1}{3}} = \frac{-\frac{1}{6}}{\frac{1}{6}} = -1\)
г) \(\frac{1-0,72}{0,72-1} = \frac{0,28}{-0,28} = -1\)
д) \(\frac{3-0,2}{0,2-3} = \frac{2,8}{-2,8} = 1\)
е) \(\frac{-(2,5-1)}{1-2,5} = \frac{-1,5}{-1,5} = 1\)
1) Для заполнения таблицы необходимо вычислить значения выражений \(a-b\) и \(b-a\) для каждого столбца. Это делается простым вычитанием: из значения \(a\) вычитаем значение \(b\), и наоборот. Например, в первом столбце \(a=11\), \(b=7\). Тогда \(a-b = 11 — 7 = 4\), а \(b-a = 7 — 11 = -4\). Аналогично вычисляем для остальных столбцов. Важно заметить, что для всех значений \(b-a\) получается число, противоположное \(a-b\). Это значит, что \(b-a = -(a-b)\) — это основная закономерность, которую нужно было найти.
| \(a\) | 11 | -4 | -2,5 | -0,5 | 0 |
| \(b\) | 7 | 5 | 10 | -0,7 | 1,6 |
| \(a-b\) | 4 | -9 | -12,5 | 0,2 | -1,6 |
| \(b-a\) | -4 | 9 | 12,5 | -0,2 | 1,6 |
2) Во второй части задачи нужно использовать эту закономерность, чтобы найти значения выражений, которые являются дробями с числителем и знаменателем, представляющими разности чисел. Например, в пункте а) выражение \(\frac{3-5}{5-3}\) можно упростить, вычислив числитель и знаменатель отдельно. Числитель \(3-5 = -2\), знаменатель \(5-3 = 2\), тогда дробь равна \(\frac{-2}{2} = -1\). Аналогично во всех пунктах числитель и знаменатель — это числа, противоположные друг другу, что ведёт к значению дроби \(-1\), за исключением пункта е), где знак минус перед скобками меняет результат на \(1\).
В пункте в) дробь состоит из разности дробных чисел: \(\frac{\frac{1}{3} — \frac{1}{2}}{\frac{1}{2} — \frac{1}{3}}\). Вычисляем числитель: \(\frac{1}{3} — \frac{1}{2} = -\frac{1}{6}\), знаменатель: \(\frac{1}{2} — \frac{1}{3} = \frac{1}{6}\). Тогда вся дробь равна \(\frac{-\frac{1}{6}}{\frac{1}{6}} = -1\). Это подтверждает общую закономерность, что дробь с числителем и знаменателем, являющимися противоположными числами, равна \(-1\).
а) \(\frac{3-5}{5-3} = \frac{-2}{2} = -1\)
б) \(\frac{0,4-0,6}{0,6-0,4} = \frac{-0,2}{0,2} = -1\)
в) \(\frac{\frac{1}{3} — \frac{1}{2}}{\frac{1}{2} — \frac{1}{3}} = \frac{-\frac{1}{6}}{\frac{1}{6}} = -1\)
г) \(\frac{1-0,72}{0,72-1} = \frac{0,28}{-0,28} = -1\)
д) \(\frac{3-0,2}{0,2-3} = \frac{2,8}{-2,8} = 1\)
е) \(\frac{-(2,5-1)}{1-2,5} = \frac{-1,5}{-1,5} = 1\)




Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!