Учебник по математике для 6-го класса авторов Дорофеева и Шарыгина — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
Что выделяет этот учебник среди других:
- Понятное изложение материала. Каждая тема объясняется простым и доступным языком, что облегчает понимание даже сложных понятий.
- Большое количество примеров и задач. Учебник предлагает разнообразные упражнения — от простых до более сложных, что помогает закрепить пройденный материал.
- Интерактивный подход. В книге есть задания, которые побуждают учеников к самостоятельному поиску решений и развитию творческого мышления.
- Связь с реальной жизнью. Многие задачи связаны с практическими ситуациями, что делает математику более живой и понятной.
- Разнообразие форм подачи информации. Здесь используются таблицы, схемы, иллюстрации, что помогает лучше усваивать материал и удерживать внимание учащихся.
ГДЗ по Математике 6 Класс Номер 911 Дорофеев, Шарыгин — Подробные Ответы
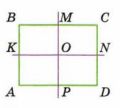
Точка О -центр симметрии прямоугольника ABCD (рис. 11.15). Прямые МР и KN перпендикулярны сторонам прямоугольника; KN = 6 см; МР= 4 см. Найдите периметр прямоугольника:
a) ABCD;
б) КВМО;
в) AKND.
а) KN = BC = AD = 6 см;
MP = AB = CD = 4 см;
Периметр ABCD равен:
4 + 6 + 4 + 6 = 10 + 10 = 20 (см).
Ответ: 20 см.
б) KO = BM = KN = 2 : 6 = 2 : 3 см;
MO = KB = MP = 2 : 4 = 2 : 2 см;
Периметр KMBO равен:
2 + 3 + 2 + 3 + 5 = 10 (см).
Ответ: 10 см.
в) KN = AD = 6 см;
OP = AK = ND = MP = 2 : 4 = 2 : 2 см;
Периметр AKND равен:
6 + 2 + 6 + 8 + 8 = 16 (см).
Ответ: 16 см.
а) KN = BC = AD = 6 см;
В данной задаче указано, что отрезки KN, BC и AD равны между собой и составляют 6 см каждый. Таким образом, это говорит о том, что фигура, которая описана в задаче, имеет стороны одинаковой длины, и периметр квадрата или прямоугольника можно вычислить, сложив длины всех его сторон.
MP = AB = CD = 4 см;
Аналогично, отрезки MP, AB и CD также равны между собой и составляют 4 см каждый. Теперь, чтобы вычислить периметр квадрата или прямоугольника ABCD, нужно просто сложить длины всех сторон:
4 + 6 + 4 + 6 = 10 + 10 = 20 (см).
Ответ: 20 см.
б) KO = BM = KN = 2 : 6 = 2 : 3 см;
Здесь указаны дополнительные отрезки KO, BM и KN, которые имеют отношение к предыдущим отрезкам. Это подразумевает, что они составляют пропорции, где длина одного отрезка составляет 2 см, а другого — 3 см. Например, KO, BM и KN равны между собой, и они составляют 2 см и 3 см, соответственно.
MO = KB = MP = 2 : 4 = 2 : 2 см;
MO, KB и MP также равны между собой, и их длина составляет 2 см и 2 см соответственно. Для расчета периметра фигуры KMBO можно сложить все ее стороны:
2 + 3 + 2 + 3 + 5 = 10 (см).
Ответ: 10 см.
в) KN = AD = 6 см;
Первая строка в этом пункте повторяет значение из предыдущих пунктов, где KN и AD равны 6 см. Это снова указывает на одинаковую длину этих отрезков.
OP = AK = ND = MP = 2 : 4 = 2 : 2 см;
Здесь описаны другие отрезки OP, AK, ND и MP, которые в сумме равны 2 см и 2 см соответственно. Эти отрезки описывают часть фигуры или строят её, образуя дополнительные стороны.
Периметр AKND равен:
6 + 2 + 6 + 8 + 8 = 16 (см).
Ответ: 16 см.
