
Учебник по математике для 6-го класса авторов Дорофеева и Шарыгина — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
ГДЗ по Математике 6 Класс Номер 888 Дорофеев, Шарыгин — Подробные Ответы
Моделируем
Между какими соседними целыми числами заключено число: \(-0,4; -2 \frac{1}{3}; -101,1; -57 \frac{5}{7}\)? Ответ запишите в виде двойного неравенства.
Подсказка. Изобразите схематически на координатной прямой данное число и ближайшие к нему слева и справа целые числа, а затем запишите двойное неравенство, например \(-6 < -5,8 < -5\).
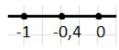
а) — \( -1 < -0,4 < 0 \);
б)- \( -102 < -101,1 < -101 \);
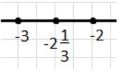
в) — \( -3 < -2 \frac{1}{3} < -2 \);
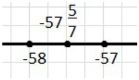
г)- \( -58 < -57 \frac{5}{7} < -57 \).
а) — \( -1 < -0,4 < 0 \);
б)- \( -102 < -101,1 < -101 \);
в) — \( -3 < -2 \frac{1}{3} < -2 \);
г)- \( -58 < -57 \frac{5}{7} < -57 \).
Для определения между какими соседними целыми числами заключено заданное число, необходимо найти два целых числа, которые расположены слева и справа от этого числа на числовой оси. Например, для числа \(-0,4\) ближайшие целые числа — это \(-1\) слева и \(0\) справа. Это значит, что \(-0,4\) находится между \(-1\) и \(0\), следовательно, двойное неравенство будет выглядеть так: \( -1 < -0,4 < 0 \).
Аналогично для числа \(-101,1\) ближайшие целые числа — это \(-102\) слева и \(-101\) справа. Число \(-101,1\) больше чем \(-102\), но меньше чем \(-101\), поэтому двойное неравенство записывается как \( -102 < -101,1 < -101 \). Это помогает понять положение числа на числовой прямой относительно целых чисел.
Для смешанных чисел, таких как \(-2 \frac{1}{3}\), нужно обратить внимание на целые числа, между которыми оно находится. В данном случае это \(-3\) слева и \(-2\) справа, так как \(-2 \frac{1}{3}\) больше чем \(-3\), но меньше чем \(-2\). Поэтому двойное неравенство будет: \( -3 < -2 \frac{1}{3} < -2 \). Аналогично для числа \(-57 \frac{5}{7}\) ближайшие целые числа — это \(-58\) слева и \(-57\) справа, значит: \( -58 < -57 \frac{5}{7} < -57 \). Такой подход позволяет точно определить расположение дробных и смешанных чисел на числовой оси.


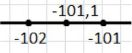


Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!