Учебник по математике для 6-го класса авторов Дорофеева и Шарыгина — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
Что выделяет этот учебник среди других:
- Понятное изложение материала. Каждая тема объясняется простым и доступным языком, что облегчает понимание даже сложных понятий.
- Большое количество примеров и задач. Учебник предлагает разнообразные упражнения — от простых до более сложных, что помогает закрепить пройденный материал.
- Интерактивный подход. В книге есть задания, которые побуждают учеников к самостоятельному поиску решений и развитию творческого мышления.
- Связь с реальной жизнью. Многие задачи связаны с практическими ситуациями, что делает математику более живой и понятной.
- Разнообразие форм подачи информации. Здесь используются таблицы, схемы, иллюстрации, что помогает лучше усваивать материал и удерживать внимание учащихся.
ГДЗ по Математике 6 Класс Номер 875 Дорофеев, Шарыгин — Подробные Ответы
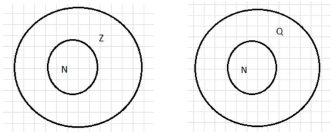
Вы знаете, как читается соотношение N ? Z: множество натуральных чисел является подмножеством множества целых чисел. Но его можно прочитать и по-другому: всякое натуральное число является целым. Прочитайте разными способами соотношения между множествами натуральных, целых и рациональных чисел и изобразите каждое из них с помощью кругов Эйлера: N ? Z, N ? Q, Z ? Q, N ? Z ? Q.
N C Z – множество натуральных чисел является подмножеством множества целых чисел, или, иначе, всякое натуральное число является целым.
N C Q – множество натуральных чисел является подмножеством множества рациональных чисел, или, иначе, всякое натуральное число является рациональным.
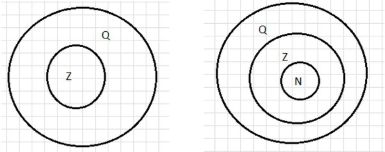
Z C Q – множество целых чисел является подмножеством множества рациональных чисел, или, иначе, всякое целое число является рациональным.
N C Z C Q – множество натуральных чисел является подмножеством множества целых чисел, которое является подмножеством множества рациональных чисел, или, иначе, всякое натуральное число является целым, а также рациональным.
N C Z – множество натуральных чисел является подмножеством множества целых чисел. Это означает, что всякое натуральное число также является целым числом. Таким образом, все числа, которые мы называем натуральными, такие как 1, 2, 3, и так далее, включены в множество целых чисел, которое состоит из всех целых чисел, как положительных, так и отрицательных.
N C Q – множество натуральных чисел является подмножеством множества рациональных чисел. Это утверждение означает, что каждое натуральное число, например 1, 2, 3 и так далее, также является рациональным числом. Рациональные числа включают в себя как целые числа, так и дроби, представляющие собой отношение двух целых чисел. Например, число 1 также можно записать как 1/1, что делает его рациональным числом.
Z C Q – множество целых чисел является подмножеством множества рациональных чисел. В данном случае, целые числа, такие как -1, 0, 1, -2, 3, и так далее, являются частью множества рациональных чисел. Это значит, что любое целое число можно выразить в виде дроби, где числитель и знаменатель — целые числа. Например, число -2 может быть записано как -2/1, что подтверждает, что оно рационально.
N C Z C Q – множество натуральных чисел является подмножеством множества целых чисел, которое в свою очередь является подмножеством множества рациональных чисел. Таким образом, всякое натуральное число является как целым, так и рациональным числом. Это утверждение подчеркивает иерархию множества натуральных чисел, целых чисел и рациональных чисел, где натуральные числа находятся на самом низком уровне, и с каждым шагом множества расширяются, включив в себя более широкие категории чисел, такие как целые и рациональные.
