ГДЗ по Математике 6 Класс Номер 873 Дорофеев, Шарыгин — Подробные Ответы

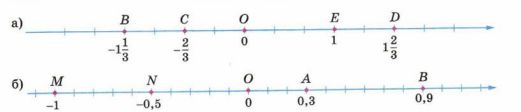
На координатной прямой (рис. 11.6, а, б) точками отмечены некоторые числа. Перечертите рисунок в тетрадь и отметьте точками противоположные им числа. Назовите координаты всех отмеченных точек.

а)
\( B\left(-1 \frac{1}{3}\right) \to B_1\left(1 \frac{1}{3}\right) \)

\( C\left(-\frac{2}{3}\right) \to C_1\left(\frac{2}{3}\right) \)

\( E(1) \to E_1(-1) \)

\( D\left(1 \frac{2}{3}\right) \to D_1\left(-1 \frac{2}{3}\right) \)

\( O(0) \)

Каждое число отражается относительно нуля, меняя знак, дробная часть и величина сохраняются. Точка \( O(0) \) остаётся на месте.

б)
\( M(-1) \to M_1(1) \)

\( N(-0,5) \to N_1(0,5) \)

\( A(0,3) \to A_1(-0,3) \)

\( B(0,9) \to B_1(-0,9) \)

\( O(0) \)

Отражение чисел относительно нуля меняет знак чисел, сохраняя их абсолютное значение. Точка \( O(0) \) не изменяется.

а) Рассмотрим преобразование точек на числовой оси. Каждая точка задана в виде числа с дробной частью, например \( -1 \frac{1}{3} \). При переходе к соответствующей точке с индексом 1 происходит отражение относительно нуля, то есть знак числа меняется на противоположный, а дробная часть сохраняется. Так, для точки \( B\left(-1 \frac{1}{3}\right) \) отражённая точка будет \( B_1\left(1 \frac{1}{3}\right) \). Аналогично для точки \( C\left(-\frac{2}{3}\right) \) отражённая точка — \( C_1\left(\frac{2}{3}\right) \).

Далее, для точки \( E(1) \) отражение относительно нуля даёт \( E_1(-1) \), то есть просто меняется знак. Точка \( D\left(1 \frac{2}{3}\right) \) отражается в точку \( D_1\left(-1 \frac{2}{3}\right) \). Точка \( O(0) \) остаётся на месте, так как ноль при отражении не меняется. Таким образом, отражение чисел относительно нуля — это операция, меняющая знак, но сохраняющая модуль числа.

б) Во втором примере аналогично рассматриваются точки, расположенные на числовой оси с десятичными дробями. Точка \( M(-1) \) отражается в \( M_1(1) \), меняя знак. Точка \( N(-0,5) \) отражается в \( N_1(0,5) \), знак меняется, величина остаётся. Точка \( A(0,3) \) отражается в \( A_1(-0,3) \), то есть знак меняется на противоположный.

Для точки \( B(0,9) \) отражённая точка — \( B_1(-0,9) \). Точка \( O(0) \) при этом остаётся без изменений, так как отражение нуля даёт ноль. Важно заметить, что отражение сохраняет расстояние точки от нуля, но меняет направление на числовой оси.

Таким образом, во всех случаях отражение точки \( x \) относительно нуля даёт точку \( x_1 = -x \). Это простое, но важное преобразование, которое меняет знак числа, не изменяя его абсолютного значения. При работе с дробными числами важно аккуратно сохранять дробную часть и знак, что и показано в данных примерах.