
Учебник по математике для 6-го класса авторов Дорофеева и Шарыгина — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
ГДЗ по Математике 6 Класс Номер 872 Дорофеев, Шарыгин — Подробные Ответы
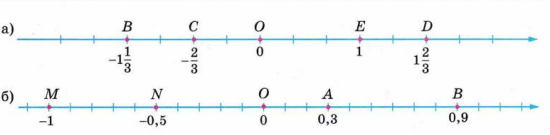
а) Начертите координатную прямую (за единичный отрезок примите 2 клетки) и отметьте на ней точками числа: \(0{,}5; 1{,}5; 2{,}5; -0{,}5; -1; -3; -3{,}5; -4{,}5.\)
б) Начертите координатную прямую с единичным отрезком, равным 6 клеткам. Отметьте на ней точками числа: \(\frac{1}{2}; \frac{2}{3}; 1 \frac{1}{3}; -\frac{1}{3}; -1; -1 \frac{1}{2}.\)
На числовой оси отмечены точки: \(-4, -3, -0{,}5, 0{,}5, 1{,}5, 2{,}5\).
б) Приводим дроби к общему знаменателю 6 и сравниваем:
\[
\frac{1}{2} = \frac{3}{6}; \quad \frac{2}{3} = \frac{4}{6}; \quad 1\frac{1}{3} = \frac{4}{3} = \frac{8}{6}; \quad \frac{1}{2} = \frac{3}{6}; \quad \frac{1}{3} = \frac{2}{6}.
\]
Расположение на числовой оси:
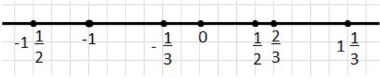
\(-1, -\frac{1}{2}, -\frac{1}{3}, 0, \frac{1}{3}, \frac{1}{2}, \frac{2}{3}, 1, \frac{4}{3}\).
а) На числовой оси показаны точки, расположенные в определённых местах на координатной прямой. Чтобы понять, где именно они находятся, нужно обратить внимание на значения, которые подписаны под точками. Например, точка, расположенная слева от нуля на отметке -4,5, соответствует числу \(-4{,}5\). Следующая точка справа — это \(-3{,}5\), затем идут точки \(-3\), \(-1\), \(-0{,}5\), \(0\), \(0{,}5\), \(1\), \(1{,}5\) и \(2{,}5\). Каждая точка занимает своё место на числовой оси, и они упорядочены по возрастанию слева направо, что соответствует увеличению числового значения.
б) Во второй части задачи представлены дроби, которые нужно привести к общему знаменателю для удобства сравнения и расположения на числовой оси. Например, дробь \(\frac{1}{2}\) можно представить в виде \(\frac{3}{6}\), умножив числитель и знаменатель на 3. Аналогично, \(\frac{2}{3}\) приводится к \(\frac{4}{6}\), умножив на 2. Это позволяет легко сравнивать дроби, так как у них теперь одинаковый знаменатель. Смешанное число \(1 \frac{1}{3}\) преобразуем в неправильную дробь: \(1 \frac{1}{3} = \frac{4}{3}\), а затем приводим к знаменателю 6, получая \(\frac{8}{6}\).
Для правильного расположения дробей на числовой оси нужно учитывать как положительные, так и отрицательные значения. Например, \(-\frac{1}{2}\) будет расположено слева от нуля, а \(\frac{1}{3}\) — справа. В итоге порядок точек на оси будет таким: \(-1, -\frac{1}{2}, -\frac{1}{3}, 0, \frac{1}{3}, \frac{1}{2}, \frac{2}{3}, 1, 1 \frac{1}{3}\). Это соответствует возрастанию значений от отрицательных к положительным. Такой подход помогает наглядно представить дроби и смешанные числа на числовой прямой, облегчая их сравнение и понимание взаимного расположения.


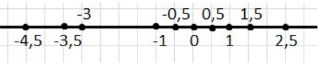


Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!