Учебник по математике для 6-го класса авторов Дорофеева и Шарыгина — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
Что выделяет этот учебник среди других:
- Понятное изложение материала. Каждая тема объясняется простым и доступным языком, что облегчает понимание даже сложных понятий.
- Большое количество примеров и задач. Учебник предлагает разнообразные упражнения — от простых до более сложных, что помогает закрепить пройденный материал.
- Интерактивный подход. В книге есть задания, которые побуждают учеников к самостоятельному поиску решений и развитию творческого мышления.
- Связь с реальной жизнью. Многие задачи связаны с практическими ситуациями, что делает математику более живой и понятной.
- Разнообразие форм подачи информации. Здесь используются таблицы, схемы, иллюстрации, что помогает лучше усваивать материал и удерживать внимание учащихся.
ГДЗ по Математике 6 Класс Номер 866 Дорофеев, Шарыгин — Подробные Ответы
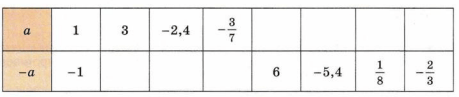
Заполните таблицу.
a 1 3 -2,4 -3/7
-a -1 6 -5,4 1/8 -2/3
| a | 1 | 3 | -2,4 | -3/7 | -6 | 5,4 | -1/8 | 2/3 |
| -a | -1 | -3 | 2,4 | 3/7 | 6 | -5,4 | 1/8 | -2/3 |
| a | 1 | 3 | -2,4 | -3/7 | -6 | 5,4 | -1/8 | 2/3 |
| -a | -1 | -3 | 2,4 | 3/7 | 6 | -5,4 | 1/8 | -2/3 |
Таблица представлена двумя строками, каждая из которых содержит значения переменной a и её противоположное значение -a.
1. В первой строке представлены значения переменной a: 1, 3, -2,4, -3/7, -6, 5,4, -1/8 и 2/3. Каждое из этих чисел представляет собой элемент, который зависит от значения переменной a, и включает целые числа, дроби и десятичные числа. Например, -2,4 и 5,4 — это десятичные числа, а -3/7 и 2/3 — дроби.
2. Во второй строке представлены значения переменной -a: -1, -3, 2,4, 3/7, 6, -5,4, 1/8 и -2/3. Эти значения противоположны значениям переменной a. Например, если a равно 1, то -a будет -1, и наоборот.
