Учебник по математике для 6-го класса авторов Дорофеева и Шарыгина — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
Что выделяет этот учебник среди других:
- Понятное изложение материала. Каждая тема объясняется простым и доступным языком, что облегчает понимание даже сложных понятий.
- Большое количество примеров и задач. Учебник предлагает разнообразные упражнения — от простых до более сложных, что помогает закрепить пройденный материал.
- Интерактивный подход. В книге есть задания, которые побуждают учеников к самостоятельному поиску решений и развитию творческого мышления.
- Связь с реальной жизнью. Многие задачи связаны с практическими ситуациями, что делает математику более живой и понятной.
- Разнообразие форм подачи информации. Здесь используются таблицы, схемы, иллюстрации, что помогает лучше усваивать материал и удерживать внимание учащихся.
ГДЗ по Математике 6 Класс Номер 860 Дорофеев, Шарыгин — Подробные Ответы
Начертите отрезок АВ и проведите через его середину прямую, ему перпендикулярную.
1) Отметьте на прямой точки С и D так, чтобы четырёхугольник ABCD был симметричен относительно прямой АВ.
2) При каком расположении точек С и D этот четырёхугольник будет иметь 2 оси симметрии? 4 оси симметрии?
1) Будет четырёхугольник ACBD.
2) При любом расположении точек C и D четырёхугольник будет иметь две оси симметрии.
Четыре оси симметрии будет в том случае, если ACBD — квадрат.
1) Будет четырёхугольник ACBD.
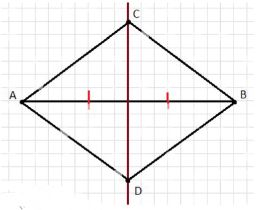
На рисунке изображён четырёхугольник ACBD, построенный на координатной сетке. Точки A и B расположены на одной горизонтали, а точки C и D — на одной вертикали относительно середины отрезка AB. Все стороны соединены прямыми линиями, образуя замкнутую фигуру — четырёхугольник.
2) При любом расположении точек C и D четырёхугольник будет иметь две оси симметрии.
Пояснение: Если точки C и D расположены симметрично относительно середины AB, то одна ось симметрии проходит через точку пересечения диагоналей, а вторая — по линии, соединяющей середины противоположных сторон. Обычно это вертикальная и горизонтальная оси.
Однако если четырёхугольник ACBD станет квадратом (то есть все его стороны и углы будут равны), то у него появятся ещё две диагональные оси симметрии, всего их станет четыре. Только в случае квадрата возможно наличие четырёх осей симметрии.
Четыре оси симметрии будет в том случае, если ACBD — квадрат.
В этом случае каждая ось делит квадрат на две равные зеркальные части, а все стороны и углы между ними равны.
