Учебник по математике для 6-го класса авторов Дорофеева и Шарыгина — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
Что выделяет этот учебник среди других:
- Понятное изложение материала. Каждая тема объясняется простым и доступным языком, что облегчает понимание даже сложных понятий.
- Большое количество примеров и задач. Учебник предлагает разнообразные упражнения — от простых до более сложных, что помогает закрепить пройденный материал.
- Интерактивный подход. В книге есть задания, которые побуждают учеников к самостоятельному поиску решений и развитию творческого мышления.
- Связь с реальной жизнью. Многие задачи связаны с практическими ситуациями, что делает математику более живой и понятной.
- Разнообразие форм подачи информации. Здесь используются таблицы, схемы, иллюстрации, что помогает лучше усваивать материал и удерживать внимание учащихся.
ГДЗ по Математике 6 Класс Номер 859 Дорофеев, Шарыгин — Подробные Ответы
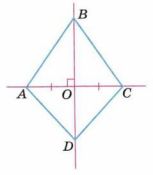
На рисунке 10.15 изображён четырёхугольник ABCD, в котором через противоположные вершины проведены прямые АС и BD.
1) Поясните, что означают знаки, которые вы видите на чертеже, и запишите условия, выражаемые данными знаками, на математическом языке.
2) Объясните, почему точки А и С симметричны относительно прямой BD.
3) Пусть АB = 5 см, AD = 3,5 см, AO = 3 см. Найдите периметр:
а) четырёхугольника АВCD;
б) треугольника АВС.
1) AO = OC; ∠AOB — прямой.
2) Точки A и C симметричны относительно прямой BD, потому что AO = OC и прямая AC перпендикулярна BD.
3) Так как точки A и C симметричны относительно прямой BD, то треугольник ABD симметричен относительно прямой BD треугольнику BCD.
а) AB = BC = 5 см; AD = CD = 3,5 см.
Периметр ABCD равен:
5 + 5 + 3,5 + 3,5 = 10 + 7 = 17 (см).
б) AB = BC = 5 см; AC = AO + OC = 3 + 3 = 6 см.
Периметр ABC равен:
5 + 5 + 6 = 16 (см).
Ответ: 17 см; 16 см.
1) AO = OC; ∠AOB — прямой.
Это значит, что отрезки AO и OC равны между собой по длине, а угол между прямыми AO и OB равен 90°, то есть он прямой.
2) Точки A и C симметричны относительно прямой BD, потому что AO = OC и прямая AC перпендикулярна BD.
Пояснение: Если две точки находятся на равных расстояниях от прямой и соединяющий их отрезок перпендикулярен этой прямой, то точки симметричны относительно данной прямой. В данном случае отрезки AO и OC равны, а прямая AC пересекает BD под прямым углом, значит, точки A и C действительно симметричны относительно прямой BD.
3) Так как точки A и C симметричны относительно прямой BD, то треугольник ABD симметричен относительно прямой BD треугольнику BCD.
Это означает, что если провести ось симметрии через прямую BD, то треугольник ABD отразится в ней и совпадёт с треугольником BCD, поскольку все соответствующие стороны и углы будут равны.
а) Пусть AB = BC = 5 см; AD = CD = 3,5 см.
Периметр четырёхугольника ABCD равен:
5 + 5 + 3,5 + 3,5 = 10 + 7 = 17 см.
Пояснение: Периметр находится как сумма длин всех сторон четырёхугольника: две стороны по 5 см и две по 3,5 см. Сложив эти значения, получаем общий периметр 17 см.
б) Пусть AB = BC = 5 см; AC = AO + OC = 3 + 3 = 6 см.
Периметр треугольника ABC равен:
5 + 5 + 6 = 16 см.
Пояснение: Для треугольника периметр вычисляется как сумма длин всех его сторон. В данном случае две стороны равны по 5 см, а третья сторона — 6 см. Суммируя, получаем периметр 16 см.
Ответ: 17 см; 16 см.
