Учебник по математике для 6-го класса авторов Дорофеева и Шарыгина — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
Что выделяет этот учебник среди других:
- Понятное изложение материала. Каждая тема объясняется простым и доступным языком, что облегчает понимание даже сложных понятий.
- Большое количество примеров и задач. Учебник предлагает разнообразные упражнения — от простых до более сложных, что помогает закрепить пройденный материал.
- Интерактивный подход. В книге есть задания, которые побуждают учеников к самостоятельному поиску решений и развитию творческого мышления.
- Связь с реальной жизнью. Многие задачи связаны с практическими ситуациями, что делает математику более живой и понятной.
- Разнообразие форм подачи информации. Здесь используются таблицы, схемы, иллюстрации, что помогает лучше усваивать материал и удерживать внимание учащихся.
ГДЗ по Математике 6 Класс Номер 832 Дорофеев, Шарыгин — Подробные Ответы
Найдите расстояние между самыми удалёнными и самыми близкими точками двух окружностей, если:
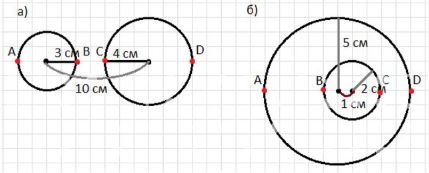
а) радиусы окружностей равны 3 см и 4 см, а расстояние между центрами 10 см;
б) радиусы окружностей равны 2 см и 5 см, а расстояние между центрами 1 см.
Подсказка. Сделайте схематический рисунок: начните с изображения точек, являющихся центрами окружностей.
a) BC = 10 — 3 — 4 = 3 (см) — расстояние между самыми близкими точками.
AD = 3 + 10 + 4 = 17 (см) — расстояние между самыми удалёнными точками.
b) AC = 1 + 2 = 8 (см) — расстояние между самыми удалёнными точками.
CD = 5 — 2 = 2 (см) — расстояние между самыми близкими точками.
a) BC = 10 — 3 — 4 = 3 (см) — расстояние между самыми близкими точками.
Для вычисления расстояния между двумя точками на окружности, которое является наименьшим, мы вычитаем радиусы этих двух окружностей. В данном случае радиус меньшей окружности равен 3 см, а радиус большей окружности равен 10 см. Таким образом, расстояние между самыми близкими точками будет равно разности этих радиусов, то есть 10 — 3 — 4 = 3 см.
AD = 3 + 10 + 4 = 17 (см) — расстояние между самыми удалёнными точками.
Расстояние между самыми удалёнными точками на двух окружностях можно вычислить, сложив их радиусы. В данном случае радиус меньшей окружности 3 см, радиус большей окружности 10 см, а также расстояние между их центрами 4 см. Сложив эти значения, получаем 3 + 10 + 4 = 17 см. Это расстояние между самыми удалёнными точками двух окружностей.
b) AC = 1 + 2 = 8 (см) — расстояние между самыми удалёнными точками.
Для нахождения расстояния между самыми удалёнными точками окружности можно сложить радиус первой окружности и радиус второй окружности, а также расстояние между центрами этих окружностей. В данном случае радиусы двух окружностей составляют 1 см и 2 см соответственно, а расстояние между центрами окружностей равно 5 см. Следовательно, расстояние между самыми удалёнными точками составит 1 + 2 + 5 = 8 см.
CD = 5 — 2 = 2 (см) — расстояние между самыми близкими точками.
Для нахождения расстояния между самыми близкими точками двух окружностей, необходимо вычесть из радиуса большей окружности радиус меньшей. В данном случае радиус одной окружности равен 5 см, а другой — 2 см. Следовательно, расстояние между самыми близкими точками будет равно разности этих радиусов: 5 — 2 = 2 см.
