
Учебник по математике для 6-го класса авторов Дорофеева и Шарыгина — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
ГДЗ по Математике 6 Класс Номер 829 Дорофеев, Шарыгин — Подробные Ответы
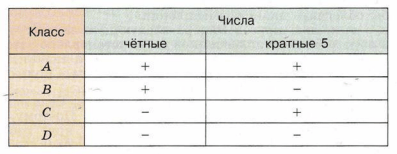
Постройте разбиение множества натуральных чисел на классы, используя два признака: чётность и кратность 5. Вам поможет следующая таблица.
Опишите словами каждый класс и приведите примеры относящихся к нему чисел.
Подсказка. А — это множество чётных чисел, кратных 5
A — множество чётных чисел, кратных 5: {10; 20; 30; …}.
B — множество чётных чисел, не кратных 5: {2; 4; 6; 8; 12; …}.
C — множество нечётных чисел, кратных 5: {5; 15; 25; 35; …}.
D — множество нечётных чисел, не кратных 5: {1; 3; 7; 9; 11; 13; …}.
A — множество чётных чисел, кратных 5:
{10; 20; 30; …} — это множество включает все чётные числа, которые делятся на 5. То есть числа, которые одновременно являются кратными 2 и 5. Примеры таких чисел: 10, 20, 30, 40, 50 и так далее. Эти числа могут быть выражены как 10n, где n — целое число, делящееся на 2 и 5 одновременно. Таким образом, они составляют арифметическую прогрессию с шагом 10, начиная с 10.
B — множество чётных чисел, не кратных 5:
{2; 4; 6; 8; 12; …} — это множество чётных чисел, которые не делятся на 5. Примеры чисел из этого множества: 2, 4, 6, 8, 12 и другие чётные числа, но не кратные 5. Например, 2 делится на 2, но не на 5, 4 также делится на 2, но не на 5, и так далее. Эти числа составляют последовательность чётных чисел, в которых нет чисел, делящихся на 5.
C — множество нечётных чисел, кратных 5:
{5; 15; 25; 35; …} — это множество чисел, которые одновременно являются нечётными и кратными 5. Примеры чисел из этого множества: 5, 15, 25, 35 и другие нечётные числа, делящиеся на 5. Эти числа можно выразить как 5(2n + 1), где n — целое число. Множество включает все нечётные числа, которые могут быть записаны как произведение 5 и нечётного числа.
D — множество нечётных чисел, не кратных 5:
{1; 3; 7; 9; 11; 13; …} — это множество нечётных чисел, которые не делятся на 5. Примеры: 1, 3, 7, 9, 11, 13 и другие нечётные числа, которые не делятся на 5. Эти числа составляют последовательность нечётных чисел, исключая те, которые делятся на 5. Например, 1 делится на 1, 3 делится на 3, 7 делится на 7, но ни одно из этих чисел не делится на 5.




Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!