Учебник по математике для 6-го класса авторов Дорофеева и Шарыгина — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
Что выделяет этот учебник среди других:
- Понятное изложение материала. Каждая тема объясняется простым и доступным языком, что облегчает понимание даже сложных понятий.
- Большое количество примеров и задач. Учебник предлагает разнообразные упражнения — от простых до более сложных, что помогает закрепить пройденный материал.
- Интерактивный подход. В книге есть задания, которые побуждают учеников к самостоятельному поиску решений и развитию творческого мышления.
- Связь с реальной жизнью. Многие задачи связаны с практическими ситуациями, что делает математику более живой и понятной.
- Разнообразие форм подачи информации. Здесь используются таблицы, схемы, иллюстрации, что помогает лучше усваивать материал и удерживать внимание учащихся.
ГДЗ по Математике 6 Класс Номер 827 Дорофеев, Шарыгин — Подробные Ответы
Какое из двух множеств является подмножеством другого:
а) A или A объединение B;
б) A или A пересечение B?
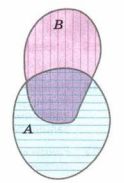
Подсказка. Воспользуйтесь рисунком 10.4
a) A ⊂ (A ∪ B).
b) A ⊃ (A ∩ B).
a) A ⊂ (A ∪ B) — это утверждение означает, что множество A является подмножеством объединения множества A и множества B. То есть все элементы множества A обязательно принадлежат объединению A и B. Это справедливо, так как объединение множества A с любым множеством B включает все элементы множества A, независимо от элементов множества B. Поэтому утверждение верно: каждый элемент множества A уже содержится в объединении A и B.
b) A ⊃ (A ∩ B) — это утверждение означает, что множество A является надмножеством пересечения множества A и множества B. То есть множество A содержит все элементы, которые принадлежат одновременно и множеству A, и множеству B, но это не означает, что все элементы пересечения принадлежат множеству A, так как в A могут быть элементы, которых нет в B. Таким образом, A обязательно включает все элементы пересечения A и B, но при этом может содержать дополнительные элементы, которых нет в B.
