Учебник по математике для 6-го класса авторов Дорофеева и Шарыгина — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
Что выделяет этот учебник среди других:
- Понятное изложение материала. Каждая тема объясняется простым и доступным языком, что облегчает понимание даже сложных понятий.
- Большое количество примеров и задач. Учебник предлагает разнообразные упражнения — от простых до более сложных, что помогает закрепить пройденный материал.
- Интерактивный подход. В книге есть задания, которые побуждают учеников к самостоятельному поиску решений и развитию творческого мышления.
- Связь с реальной жизнью. Многие задачи связаны с практическими ситуациями, что делает математику более живой и понятной.
- Разнообразие форм подачи информации. Здесь используются таблицы, схемы, иллюстрации, что помогает лучше усваивать материал и удерживать внимание учащихся.
ГДЗ по Математике 6 Класс Номер 825 Дорофеев, Шарыгин — Подробные Ответы
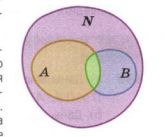
На рисунке 10.7 большой круг изображает множество натуральных чисел N, а два малых — его подмножества: A — множество чисел, делящихся на 2, B — множество чисел, делящихся на 3. Большой круг разбивается малыми на четыре области. (Они закрашены разными цветами.) Какие числа соответствуют каждой из этих областей? Опишите их словами и приведите примеры.
Фиолетовая область — {1; 5; 7; 11; 13; 17; …} — множество натуральных чисел, не делящихихся ни на 2, ни на 3;
Желтая область — {2; 4; 8; 10; 14; 16; …} — множество чётных чисел, не делящихся на 3;
Синяя область — {3; 9; 15; 21; 27; …} — множество чисел, кратных 3, но не делящихихся на 2;
Зеленая область — {6; 12; 18; 24; 30; …} — множество чисел, кратных 6.
Фиолетовая область — {1; 5; 7; 11; 13; 17; …} — это множество натуральных чисел, которые не делятся ни на 2, ни на 3. Это означает, что каждый элемент в этом множестве — простое число, которое не может быть поделено на 2 или 3 без остатка. Например: 1, 5, 7, 11, 13 и 17 — все эти числа не делятся на 2 или 3. Это множество состоит из чисел, которые находятся на пересечении чисел, не делящихся на 2 и чисел, не делящихся на 3. Можно заметить, что эти числа являются нечётными, но важно подчеркнуть, что они не образуют стандартную арифметическую прогрессию.
Желтая область — {2; 4; 8; 10; 14; 16; …} — это множество чётных чисел, которые не делятся на 3. Числа из этого множества чётные (то есть делятся на 2), но при этом не делятся на 3. Например, 2, 4, 8, 10, 14 и 16 — все эти числа делятся на 2, но не делятся на 3. Множество включает все такие числа, которые могут быть выражены как 2n, где n — целое число, но для которых сумма цифр не делится на 3. Эти числа образуют арифметическую прогрессию с шагом 2, начиная с 2.
Синяя область — {3; 9; 15; 21; 27; …} — это множество чисел, которые кратны 3, но не делятся на 2. Эти числа образуют арифметическую прогрессию с шагом 6, начиная с 3. Все элементы множества являются кратными 3, но они не чётные, то есть не делятся на 2. Примером такого множества могут быть числа: 3, 9, 15, 21, 27 и так далее. Каждое из этих чисел делится на 3, но не является чётным.
Зеленая область — {6; 12; 18; 24; 30; …} — это множество чисел, которые одновременно кратны и 2, и 3, то есть кратны 6. Эти числа образуют арифметическую прогрессию с шагом 6, начиная с 6. Каждое число из этого множества делится как на 2, так и на 3. Например: 6, 12, 18, 24 и 30 — все эти числа кратны 6. Они являются одновременно чётными и кратными 3. Это множество представляет собой пересечение чётных чисел и чисел, кратных 3.
