Учебник по математике для 6-го класса авторов Дорофеева и Шарыгина — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
Что выделяет этот учебник среди других:
- Понятное изложение материала. Каждая тема объясняется простым и доступным языком, что облегчает понимание даже сложных понятий.
- Большое количество примеров и задач. Учебник предлагает разнообразные упражнения — от простых до более сложных, что помогает закрепить пройденный материал.
- Интерактивный подход. В книге есть задания, которые побуждают учеников к самостоятельному поиску решений и развитию творческого мышления.
- Связь с реальной жизнью. Многие задачи связаны с практическими ситуациями, что делает математику более живой и понятной.
- Разнообразие форм подачи информации. Здесь используются таблицы, схемы, иллюстрации, что помогает лучше усваивать материал и удерживать внимание учащихся.
ГДЗ по Математике 6 Класс Номер 817 Дорофеев, Шарыгин — Подробные Ответы
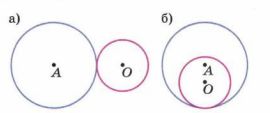
Радиусы окружностей равны 5 см и 3 см (рис. 10.3, а, б). Чему равно расстояние между их центрами?
а) AO = 5 + 3 = 8 см.
б) AO = 5 — 3 = 2 см.
а) AO = 5 + 3 = 8 см. — Это выражение описывает, как мы находим расстояние между двумя точками. В данном случае, от точки O до точки A можно пройти сначала 5 см, а затем ещё 3 см, что в сумме даёт 8 см. Это типичный пример сложения длин отрезков, когда путь между точками складывается из нескольких частей.
б) AO = 5 — 3 = 2 см. — Здесь мы рассматриваем другую ситуацию, где, например, точка O находится ближе к точке A, и нам нужно вычесть длину одного отрезка из другого. Если сначала расстояние между точками составляет 5 см, а потом мы убираем 3 см, то оставшаяся длина пути составит 2 см. Это пример вычитания длин отрезков, когда один отрезок убирает часть длины другого.
