Учебник по математике для 6-го класса авторов Дорофеева и Шарыгина — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
Что выделяет этот учебник среди других:
- Понятное изложение материала. Каждая тема объясняется простым и доступным языком, что облегчает понимание даже сложных понятий.
- Большое количество примеров и задач. Учебник предлагает разнообразные упражнения — от простых до более сложных, что помогает закрепить пройденный материал.
- Интерактивный подход. В книге есть задания, которые побуждают учеников к самостоятельному поиску решений и развитию творческого мышления.
- Связь с реальной жизнью. Многие задачи связаны с практическими ситуациями, что делает математику более живой и понятной.
- Разнообразие форм подачи информации. Здесь используются таблицы, схемы, иллюстрации, что помогает лучше усваивать материал и удерживать внимание учащихся.
ГДЗ по Математике 6 Класс Номер 813 Дорофеев, Шарыгин — Подробные Ответы
О множествах A, B и C известно, что A ? B и A ? C. Сделайте вывод о множествах B и C, ответив на вопросы:
1) Может ли одно из этих множеств быть подмножеством другого, и если да, то какие могут быть варианты?
2) Может ли ни одно из этих множеств не являться подмножеством другого?
Для всех возможных случаев приведите примеры.
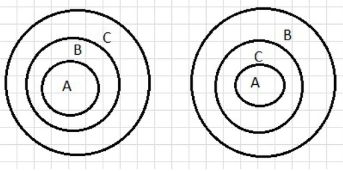
1) Может: A ⊆ B ⊆ C или A ⊆ C ⊆ B, тогда B ⊆ C или C ⊆ B. — В этом случае описаны два возможных отношения между множествами A, B и C. Первое отношение говорит о том, что A является подмножеством B, а B, в свою очередь, подмножеством C. Во втором случае A является подмножеством C, а C подмножеством B. В обоих случаях возможны обратные отношения, где B является подмножеством C, или наоборот.
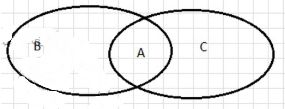
2) Может: B ∉ C; C ∉ B. — Это выражение указывает на то, что множества B и C не являются подмножествами друг друга. То есть, элементы множества B не принадлежат множеству C, и наоборот, элементы множества C не принадлежат множеству B. Это может происходить, если множества пересекаются, но одно не является частью другого, как показано на схематическом изображении, где два множества частично пересекаются, но не включают друг друга.
1) Может: A ⊆ B ⊆ C или A ⊆ C ⊆ B, тогда B ⊆ C или C ⊆ B. — В этом случае рассмотрены два возможных типа отношений между множествами A, B и C. Первое утверждение указывает на то, что множество A является подмножеством множества B, а множество B в свою очередь является подмножеством множества C. Это означает, что все элементы множества A находятся в множестве B, и все элементы множества B находятся в множестве C. Если это так, то и множество B может быть подмножеством C или наоборот. Второе утверждение говорит о том, что A может быть подмножеством C, а C подмножеством B. Это более сложное взаимодействие, но оно также допускает возможность обратных отношений, при которых B является подмножеством C, или C — подмножеством B.
Эти отношения показывают, что множество A может быть полностью вложено в множество B или C, и что B и C могут либо включать друг друга, либо быть независимыми, в зависимости от структуры их элементов. Визуально это можно представить как три круги, где один круг полностью внутри другого или два круга пересекаются, но не содержат друг друга целиком.
2) Может: B ∉ C; C ∉ B. — Это выражение подразумевает, что множества B и C не являются подмножествами друг друга. То есть, ни одно из этих множеств не входит в другое. В этом случае множества могут пересекаться, но не быть вложенными друг в друга. Например, элементы множества B могут пересекаться с элементами множества C, но ни одно множество не является частью другого. Такое отношение между множествами часто встречается в реальной жизни, например, когда два множества содержат общие элементы, но также имеют свои уникальные элементы, которые не принадлежат другому множеству. Визуально это можно представить как два перекрывающихся круга, где части этих кругов пересекаются, но ни одно множество не входит полностью в другое.
Эти два случая показывают разные типы отношений между множествами: одно может быть частью другого, или они могут пересекаться, но не быть подмножествами друг друга. Важно понимать, что понятие подмножества или пересечения помогает нам анализировать структуры данных и отношения между различными категориями элементов.
