Учебник по математике для 6-го класса авторов Дорофеева и Шарыгина — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
Что выделяет этот учебник среди других:
- Понятное изложение материала. Каждая тема объясняется простым и доступным языком, что облегчает понимание даже сложных понятий.
- Большое количество примеров и задач. Учебник предлагает разнообразные упражнения — от простых до более сложных, что помогает закрепить пройденный материал.
- Интерактивный подход. В книге есть задания, которые побуждают учеников к самостоятельному поиску решений и развитию творческого мышления.
- Связь с реальной жизнью. Многие задачи связаны с практическими ситуациями, что делает математику более живой и понятной.
- Разнообразие форм подачи информации. Здесь используются таблицы, схемы, иллюстрации, что помогает лучше усваивать материал и удерживать внимание учащихся.
ГДЗ по Математике 6 Класс Номер 812 Дорофеев, Шарыгин — Подробные Ответы
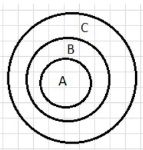
О множествах А, В и С известно, что A ? B или B ? C. Какое соотношение связывает множества A и C? Проиллюстрируйте свой ответ рисунком.
A ⊆ C — это выражение означает, что множество A является подмножеством множества C. То есть все элементы множества A находятся в множестве C, но множество C может содержать дополнительные элементы, которых нет в A. В графическом представлении это означает, что круг, представляющий A, полностью содержится внутри круга, представляющего C.
A ⊆ C — это выражение означает, что множество A является подмножеством множества C. Это утверждение подразумевает, что все элементы, принадлежащие множеству A, также принадлежат множеству C. Однако множество C может содержать дополнительные элементы, которых нет в A, что делает C более широким множеством по сравнению с A. В графическом представлении, которое вы видите, круг, представляющий множество A, полностью находится внутри круга, который представляет множество C, что визуально показывает, что A является частью C, но не обязательно совпадает с ним.
Пример: если A — это множество всех четных чисел от 1 до 10 (A = {2, 4, 6, 8}), а C — это множество всех чисел от 1 до 10 (C = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}), то множество A является подмножеством множества C, так как все четные числа из A входят в C, но C также содержит нечетные числа, которых нет в A.
Таким образом, отношение подмножества показывает, что элементы одного множества всегда находятся внутри другого множества, но не обязательно наоборот. Это важная концепция в теории множеств, позволяющая упорядочить и структурировать элементы множества и их взаимоотношения.
