Учебник по математике для 6-го класса авторов Дорофеева и Шарыгина — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
Что выделяет этот учебник среди других:
- Понятное изложение материала. Каждая тема объясняется простым и доступным языком, что облегчает понимание даже сложных понятий.
- Большое количество примеров и задач. Учебник предлагает разнообразные упражнения — от простых до более сложных, что помогает закрепить пройденный материал.
- Интерактивный подход. В книге есть задания, которые побуждают учеников к самостоятельному поиску решений и развитию творческого мышления.
- Связь с реальной жизнью. Многие задачи связаны с практическими ситуациями, что делает математику более живой и понятной.
- Разнообразие форм подачи информации. Здесь используются таблицы, схемы, иллюстрации, что помогает лучше усваивать материал и удерживать внимание учащихся.
ГДЗ по Математике 6 Класс Номер 778 Дорофеев, Шарыгин — Подробные Ответы
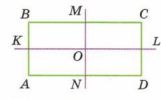
Прямые KL и МN — оси симметрии прямоугольника ABCD (рис. 9.9). Известно, что АN = 4,5 см и CL = 2,5 см. Найдите:
а) периметр прямоугольника КВМО;
б) периметр прямоугольника AKLD;
в) периметр прямоугольника ABCD;
г) длину ломаной ANMCD.
a) AN = KO = BM = 4,5 см;
CL = BK = MO = 2,5 см.
Периметр KBMO равен:
2 * (4,5 + 2,5) = 2 * 7 = 14 см.
Ответ: 14 см.
b) AD = KL = AN + ND = 4,5 + 4,5 = 9 см.
CL = LD = AK = 2,5 см.
Периметр AKLD равен:
2 * (9 + 2,5) = 2 * 11,5 = 23 см.
Ответ: 23 см.
в) AD = BC = AN + ND = 4,5 + 4,5 = 9 см.
CD = AB = CL + LD = 2,5 + 2,5 = 5 см.
Периметр ABCD равен:
2 * (9 + 5) = 2 * 14 = 28 см.
Ответ: 28 см.
г) NM = CD = CL = LD = 2,5 + 2,5 = 5 см.
AN = 4,5 см.
Длина ломаной ANMCD равна:
4,5 + 5 + 5 + 5 = 9 + 10 = 19 см.
Ответ: 19 см.
a) AN = KO = BM = 4,5 см. Это означает, что длины отрезков AN, KO и BM равны и составляют 4,5 см каждый. Также даны следующие равенства:
CL = BK = MO = 2,5 см. Это говорит нам, что отрезки CL, BK и MO тоже равны между собой и составляют 2,5 см.
Теперь давайте вычислим периметр четырёхугольника KBMO, который составляют отрезки KB, BM, MO и OK. Периметр вычисляется как сумма всех сторон:
Периметр KBMO равен:
2 * (4,5 + 2,5) = 2 * 7 = 14 см.
Ответ: 14 см.
b) AD = KL = AN + ND = 4,5 + 4,5 = 9 см. Это означает, что длины отрезков AD и KL равны и составляют 9 см, так как они складываются из двух одинаковых частей (AN и ND), каждая из которых равна 4,5 см.
CL = LD = AK = 2,5 см. Эти отрезки также равны и составляют 2,5 см каждый.
Периметр четырёхугольника AKLD будет равен сумме длин его сторон. Рассчитаем периметр:
Периметр AKLD равен:
2 * (9 + 2,5) = 2 * 11,5 = 23 см.
Ответ: 23 см.
в) AD = BC = AN + ND = 4,5 + 4,5 = 9 см. Это утверждение аналогично предыдущему, так как AD и BC имеют одинаковую длину, равную 9 см.
CD = AB = CL + LD = 2,5 + 2,5 = 5 см. Эти отрезки равны и составляют 5 см каждый.
Теперь вычислим периметр четырёхугольника ABCD, который состоит из отрезков AD, BC, CD и AB. Сложим все длины сторон:
Периметр ABCD равен:
2 * (9 + 5) = 2 * 14 = 28 см.
Ответ: 28 см.
г) NM = CD = CL = LD = 2,5 + 2,5 = 5 см. Эти отрезки равны и составляют 5 см каждый.
AN = 4,5 см. Это длина отрезка AN, которая дана в условиях задачи.
Наша цель — вычислить длину ломаной ANMCD, которая состоит из отрезков AN, NM, CD и LD. Рассчитаем сумму длин этих отрезков:
Длина ломаной ANMCD равна:
4,5 + 5 + 5 + 5 = 9 + 10 = 19 см.
Ответ: 19 см.
научились
