Учебник по математике для 6-го класса авторов Дорофеева и Шарыгина — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
Что выделяет этот учебник среди других:
- Понятное изложение материала. Каждая тема объясняется простым и доступным языком, что облегчает понимание даже сложных понятий.
- Большое количество примеров и задач. Учебник предлагает разнообразные упражнения — от простых до более сложных, что помогает закрепить пройденный материал.
- Интерактивный подход. В книге есть задания, которые побуждают учеников к самостоятельному поиску решений и развитию творческого мышления.
- Связь с реальной жизнью. Многие задачи связаны с практическими ситуациями, что делает математику более живой и понятной.
- Разнообразие форм подачи информации. Здесь используются таблицы, схемы, иллюстрации, что помогает лучше усваивать материал и удерживать внимание учащихся.
ГДЗ по Математике 6 Класс Номер 758 Дорофеев, Шарыгин — Подробные Ответы
Пусть a и b — целые числа. Покажите, как они могут быть расположены на координатной прямой (сделайте рисунок для каждого случая), если известно, что:
1) a — отрицательное число и b < а;
2) a — отрицательное число и b > а;
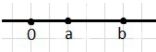
3) а — положительное число и b > а;
4) а — положительное число и b < а.
Какой вывод можно сделать о числе b в каждом из этих случаев?
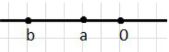
1) a < 0, b < a:
Здесь b — отрицательное число. На графике показано, что число a расположено слева от нуля, а число b находится еще левее, что соответствует тому, что b меньше a и отрицательно.
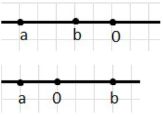
2) a < 0, b > a:
Здесь b — положительное или отрицательное число, или b = 0. На графике показано, что a расположено слева от нуля, а b находится правее a, то есть b больше a, но может быть как положительным, так и равным нулю.
3) b < a:
Здесь b — положительное число. Это означает, что число b расположено слева от числа a, и b всегда положительно, как показано на графике.
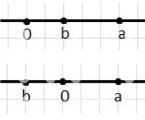
4) a > 0, b < a:
Здесь b — положительное или отрицательное число, или b = 0. На графике показано, что a больше нуля, и b расположено левее a, то есть b меньше a, но может быть как положительным, так и равным нулю.
1) a < 0, b < a:
В данном случае a — отрицательное число, и b также отрицательное. Число b расположено слева от a на числовой оси, поскольку b меньше a. Это означает, что b — более отрицательное число по сравнению с a. Визуально это изображено на графике, где оба числа находятся слева от нуля, но b находится еще дальше от него, показывая, что b имеет меньшую (большую по абсолютной величине) величину. Таким образом, b — отрицательное число, которое по модулю больше, чем a.
2) a < 0, b > a:
Здесь a — отрицательное число, а b больше, чем a, то есть b расположено правее на числовой оси по сравнению с a. Важно отметить, что b может быть как положительным числом, так и отрицательным числом, но при этом b больше, чем a. Это также может означать, что b равно нулю, так как ноль больше любого отрицательного числа. На графике видно, что число b расположено справа от a, что и подтверждает его большее значение по сравнению с a.
3) b < a:
В этом случае b — положительное число, и оно всегда меньше числа a. Это означает, что на числовой оси b будет находиться слева от числа a. Такое положение чисел предполагает, что число a положительное и больше числа b. На графике можно увидеть, что b расположено слева от a, а это соответствует положению чисел на оси, где более высокие числа располагаются правее, а более низкие — слева. В данном случае a всегда будет больше, чем b.
4) a > 0, b < a:
Здесь a — положительное число, и b меньше a. Число b расположено слева от числа a на числовой оси, так как оно меньше. Однако b может быть как отрицательным числом, так и положительным, но меньшим, чем a, или равным нулю. На графике видно, что число a находится правее нуля, а число b расположено левее, что подтверждает, что b меньше a. Важно, что число b может быть как положительным, так и отрицательным, но оно всегда будет меньшим, чем число a.
