Учебник по математике для 6-го класса авторов Дорофеева и Шарыгина — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
Что выделяет этот учебник среди других:
- Понятное изложение материала. Каждая тема объясняется простым и доступным языком, что облегчает понимание даже сложных понятий.
- Большое количество примеров и задач. Учебник предлагает разнообразные упражнения — от простых до более сложных, что помогает закрепить пройденный материал.
- Интерактивный подход. В книге есть задания, которые побуждают учеников к самостоятельному поиску решений и развитию творческого мышления.
- Связь с реальной жизнью. Многие задачи связаны с практическими ситуациями, что делает математику более живой и понятной.
- Разнообразие форм подачи информации. Здесь используются таблицы, схемы, иллюстрации, что помогает лучше усваивать материал и удерживать внимание учащихся.
ГДЗ по Математике 6 Класс Номер 677 Дорофеев, Шарыгин — Подробные Ответы
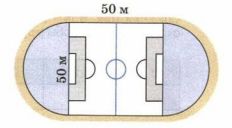
На рисунке 8.17 изображён план школьного стадиона, вокруг которого проложена беговая дорожка. Найдите длину дорожки и площадь стадиона. (Полученные числовые значения округлите до десятков.)
1) Длина двух полуокружностей:
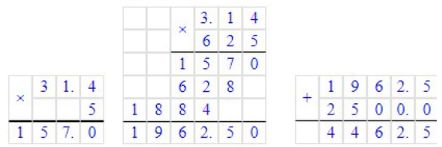
C = πd = 3,14 * 50 = 157 (м).
2) Длина дорожки равна:
157 + 50 + 50 + 100 = 257 ≈ 260 (м).
3) Радиус окружностей равен:
50 : 2 = 25 (м).
4) Площадь двух полуокружностей:
S = πr² = 3,14 * 25² = 3,14 * 625 = 1962,5 (м²).
5) Площадь стадиона:
1962,5 + 2500 = 4462,5 ≈ 4460 (м²).
Задача о расчёте длины и площади дорожки, которая состоит из двух полуокружностей и двух отрезков. Рассмотрим каждый шаг решения задачи:
1) Длина двух полуокружностей:
Для вычисления длины полуокружности используется формула:
C = πd,
где C — длина окружности, а d — диаметр.
Для двух полуокружностей, где диаметр равен 50 м:
C = 3,14 * 50 = 3,14 * 50 = 157 м.
Таким образом, длина двух полуокружностей составляет 157 м.
2) Длина дорожки:
Длина дорожки состоит из длины двух полуокружностей и двух отрезков:
Длина дорожки = 157 + 50 + 50 + 100 = 257 ≈ 260 м.
Таким образом, длина дорожки равна 260 м.
3) Радиус окружностей:
Известно, что диаметр окружности равен 50 м, следовательно, радиус окружности равен:
50 : 2 = 25 м.
Таким образом, радиус окружности составляет 25 м.
4) Площадь двух полуокружностей:
Для вычисления площади двух полуокружностей используем формулу площади круга:
S = πr²,
где S — площадь круга, r — радиус.
Площадь одного круга с радиусом 25 м:
S = 3,14 * 25² = 3,14 * 625 = 1962,5 м².
Площадь двух полуокружностей будет в два раза больше площади одного круга:
Площадь двух полуокружностей = 2 * 1962,5 = 3925 м².
5) Площадь стадиона:
Площадь стадиона состоит из площади двух полуокружностей и площади прямоугольника, для которого длина одной стороны равна 50 м, а другая — 100 м:
Площадь прямоугольника = 50 * 50 = 2500 м².
Площадь стадиона = 1962,5 + 2500 = 4462,5 ≈ 4460 м².
Таким образом, площадь стадиона составляет 4460 м².
