ГДЗ по Математике 6 Класс Номер 657 Дорофеев, Шарыгин — Подробные Ответы

В кинозале n рядов по k кресел в каждом ряду. Число мест в кинозале можно вычислить по формуле N = kn.
1) Сколько мест в кинозале, если:
а) k = 10, n = 12;
б) k = 33, n = 25?
2) Сколько в кинозале рядов, если в каждом ряду 15 кресел, а всего в кинозале 300 мест? Выразите n через N и k.
3) Сколько кресел в каждом ряду, если всего в кинозале 176 мест и 11 рядов? Выразите k через N и n.

\(N = kn\) — число мест в кинозале.

1)
a) \(k = 10; \quad n = 12;\)
\(N = 10 \cdot 12 = 120\) (мест).

б) \(k = 33; \quad n = 25;\)
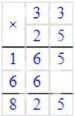
\(N = 33 \cdot 25 = 825\) (мест).

2) \(n = \frac{N}{k}\) — рядов в кинозале.
\(k = 15; \quad N = 300;\)
\(n = \frac{300}{15} = 20\) (рядов).

3) \(k = \frac{N}{n}\) — кресел в кинозале.
\(N = 176; \quad n = 11;\)
\(k = \frac{176}{11} = 16\) (кресел).

\(N = kn\) — формула, которая показывает, что общее число мест \(N\) в кинозале равно произведению количества кресел в одном ряду \(k\) на количество рядов \(n\). Это основное уравнение для вычисления вместимости зала.

1)
a) Если в одном ряду \(k = 10\) кресел, а рядов всего \(n = 12\), то общее число мест вычисляется как произведение этих чисел:
\(N = 10 \cdot 12 = 120\). Это значит, что в кинозале всего 120 мест. Здесь мы просто умножили количество кресел в ряду на количество рядов, чтобы получить итоговое количество мест.

б) Если количество кресел в ряду увеличивается до \(k = 33\), а рядов становится \(n = 25\), то общее количество мест будет:
\(N = 33 \cdot 25 = 825\). Таким образом, при увеличении как количества кресел в ряду, так и числа рядов, общее число мест значительно возрастает.

2) Для нахождения количества рядов \(n\) в кинозале, если известно общее число мест \(N\) и количество кресел в одном ряду \(k\), используется формула:
\(n = \frac{N}{k}\). Это значит, что количество рядов равно общему числу мест, делённому на количество кресел в ряду.

Если, например, в кинозале всего \(N = 300\) мест, а в одном ряду по \(k = 15\) кресел, то количество рядов будет:
\(n = \frac{300}{15} = 20\). Значит, в таком зале 20 рядов.

3) Чтобы найти количество кресел в одном ряду \(k\), если известно общее число мест \(N\) и количество рядов \(n\), используется формула:
\(k = \frac{N}{n}\). Это означает, что количество кресел в ряду равно общему количеству мест, делённому на число рядов.

Если в кинозале всего \(N = 176\) мест и имеется \(n = 11\) рядов, то количество кресел в каждом ряду будет:
\(k = \frac{176}{11} = 16\). Таким образом, в каждом ряду по 16 кресел.