Учебник по математике для 6-го класса авторов Дорофеева и Шарыгина — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
Что выделяет этот учебник среди других:
- Понятное изложение материала. Каждая тема объясняется простым и доступным языком, что облегчает понимание даже сложных понятий.
- Большое количество примеров и задач. Учебник предлагает разнообразные упражнения — от простых до более сложных, что помогает закрепить пройденный материал.
- Интерактивный подход. В книге есть задания, которые побуждают учеников к самостоятельному поиску решений и развитию творческого мышления.
- Связь с реальной жизнью. Многие задачи связаны с практическими ситуациями, что делает математику более живой и понятной.
- Разнообразие форм подачи информации. Здесь используются таблицы, схемы, иллюстрации, что помогает лучше усваивать материал и удерживать внимание учащихся.
ГДЗ по Математике 6 Класс Номер 654 Дорофеев, Шарыгин — Подробные Ответы
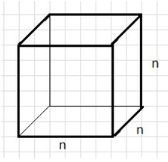
1) Начертите куб. Обозначьте длину его ребра какой-нибудь буквой и составьте формулу объёма куба.
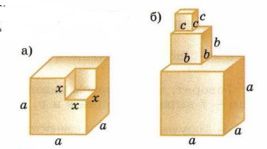
2) Запишите формулы для вычисления объёма фигуры, изображённой на рисунке 8.9, а,б.
1) V = n · n · n = n³.
2) a) V = a³ — x³.
б) V = a³ + b³ + c³.
1) Формула: V = n · n · n = n³.
Это выражение описывает объём куба с длиной ребра n. В данном случае, объём куба равен произведению длины всех трёх его рёбер, так как у куба все рёбра равны. Мы умножаем длину ребра n на себя трижды, что даёт выражение n³, то есть объём куба равен n³.
2) a) Формула: V = a³ — x³.
Это выражение может быть использовано для вычисления разности объёмов двух тел, где одно из тел имеет объём a³, а другое — объём x³. Например, это может быть полезно для вычисления объёма полости, оставшейся после выемки одного объекта из другого, если оба объекта имеют форму кубов.
б) Формула: V = a³ + b³ + c³.
Это выражение может быть использовано для вычисления суммы объёмов нескольких тел. Если у нас есть три объекта, каждый из которых имеет объём, вычисляемый по формуле для куба, с длинами рёбер a, b и c, то общий объём этих объектов равен a³ + b³ + c³.
