Учебник по математике для 6-го класса авторов Дорофеева и Шарыгина — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
Что выделяет этот учебник среди других:
- Понятное изложение материала. Каждая тема объясняется простым и доступным языком, что облегчает понимание даже сложных понятий.
- Большое количество примеров и задач. Учебник предлагает разнообразные упражнения — от простых до более сложных, что помогает закрепить пройденный материал.
- Интерактивный подход. В книге есть задания, которые побуждают учеников к самостоятельному поиску решений и развитию творческого мышления.
- Связь с реальной жизнью. Многие задачи связаны с практическими ситуациями, что делает математику более живой и понятной.
- Разнообразие форм подачи информации. Здесь используются таблицы, схемы, иллюстрации, что помогает лучше усваивать материал и удерживать внимание учащихся.
ГДЗ по Математике 6 Класс Номер 652 Дорофеев, Шарыгин — Подробные Ответы
Рассуждаем.
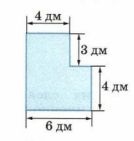
1) Чтобы найти площадь многоугольника, изображённого на рисунке 8.6, его можно разбить на прямоугольники и вычислить результат сложения площадей или достроить его до прямоугольника и вычислить результат вычитанием площадей. Вычислите площадь двумя способами.
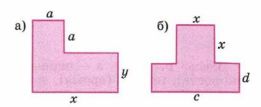
2) Составьте формулы для вычисления площади фигуры (рис. 8.7, а, б)
1) С = 4 · 3 + 4 · 6 = 12 + 24 = 36 (дм²).
С = 6 · (3 + 4) — 3 · (6 — 4) = 6 · 7 — 3 · 2 = 42 — 6 = 36 (дм²).
2) a) S = a · a + xy = a² + xy.
б) S = cd + x · x = cd + x².
1) С = 4 · 3 + 4 · 6 = 12 + 24 = 36 (дм²).
Здесь мы видим, как рассчитывается площадь прямоугольника. Сначала умножаем длину на ширину: 4 · 3 и 4 · 6, затем складываем полученные результаты: 12 + 24, что даёт итоговую площадь 36 дм².
Дальше рассматриваем другое вычисление, которое также приводит к той же площади: S = 6 · (3 + 4) — 3 · (6 — 4) = 6 · 7 — 3 · 2 = 42 — 6 = 36 (дм²). Здесь применяются сначала скобки для суммирования и вычитания, а затем выполняются умножения и вычитания, результат также равен 36 дм².
2) a) Формула для вычисления площади прямоугольника с дополнительными переменными: S = a · a + xy = a² + xy.
В этой формуле мы видим, что площадь прямоугольника вычисляется как произведение одной стороны на саму себя, плюс дополнительный член xy, который может обозначать какой-либо другой параметр. Эта формула используется, если нужно учесть дополнительные размеры или переменные.
б) Формула для площади прямоугольника с другой переменной: S = cd + x · x = cd + x².
Здесь у нас другая формула, в которой переменные cd и x · x обозначают произведение сторон и квадрат какой-то дополнительной переменной. Это также может быть полезно для расчётов с более сложными геометрическими фигурами или дополнительными параметрами.
