Учебник по математике для 6-го класса авторов Дорофеева и Шарыгина — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
Что выделяет этот учебник среди других:
- Понятное изложение материала. Каждая тема объясняется простым и доступным языком, что облегчает понимание даже сложных понятий.
- Большое количество примеров и задач. Учебник предлагает разнообразные упражнения — от простых до более сложных, что помогает закрепить пройденный материал.
- Интерактивный подход. В книге есть задания, которые побуждают учеников к самостоятельному поиску решений и развитию творческого мышления.
- Связь с реальной жизнью. Многие задачи связаны с практическими ситуациями, что делает математику более живой и понятной.
- Разнообразие форм подачи информации. Здесь используются таблицы, схемы, иллюстрации, что помогает лучше усваивать материал и удерживать внимание учащихся.
ГДЗ по Математике 6 Класс Номер 649 Дорофеев, Шарыгин — Подробные Ответы
Выполните следующие построения на альбомном листе бумаги:
1) Начертите отрезок AB длиной б см.
2) Проведите окружность с центром в точке А, радиус которой равен 4 см.
3) Проведите две окружности с центром в точке В, которые касаются первой окружности внешним и внутренним образом. Чему равны их радиусы?
1) Начертите отрезок AB длиной 8 см.
Для этого используйте линейку и отложите отрезок, длина которого равна 8 см, обозначив его точки как A и B.
2) Проведите окружность с центром в точке A, радиус которой равен 4 см.
Используя циркуль, поставьте иглу в точку A и отложите радиус 4 см. Проведите окружность, которая будет иметь центр в точке A и радиус 4 см.
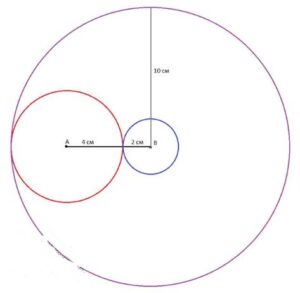
3) Проведите две окружности с центром в точке B, которые касаются первой окружности внешним и внутренним образом. Чему равны их радиусы?
Предположим, радиус первой окружности — 4 см. Для того чтобы провести две окружности с центром в точке B, которые касаются первой окружности внешним и внутренним образом, используем следующую теорему:
- Если две окружности касаются внешним образом, то расстояние между их центрами равно сумме их радиусов.
- Если две окружности касаются внутренним образом, то расстояние между их центрами равно разности их радиусов.
Обозначим радиусы искомых окружностей как r₁ и r₂.
- Для внешнего касания: r₁ + r₂ = 4 см (сумма радиусов первой окружности и одной из искомых окружностей).
- Для внутреннего касания: |r₁ — r₂| = 4 см (разность радиусов первой окружности и второй искомой окружности).
Решив эту систему уравнений, получаем, что радиусы искомых окружностей равны: r₁ = 2 см и r₂ = 2 см. Эти радиусы соответствуют внутреннему и внешнему касанию.
