Учебник по математике для 6-го класса авторов Дорофеева и Шарыгина — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
Что выделяет этот учебник среди других:
- Понятное изложение материала. Каждая тема объясняется простым и доступным языком, что облегчает понимание даже сложных понятий.
- Большое количество примеров и задач. Учебник предлагает разнообразные упражнения — от простых до более сложных, что помогает закрепить пройденный материал.
- Интерактивный подход. В книге есть задания, которые побуждают учеников к самостоятельному поиску решений и развитию творческого мышления.
- Связь с реальной жизнью. Многие задачи связаны с практическими ситуациями, что делает математику более живой и понятной.
- Разнообразие форм подачи информации. Здесь используются таблицы, схемы, иллюстрации, что помогает лучше усваивать материал и удерживать внимание учащихся.
ГДЗ по Математике 6 Класс Номер 606 Дорофеев, Шарыгин — Подробные Ответы
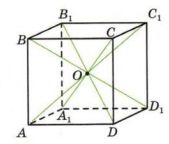
Центр куба — это точка пересечения его диагоналей (рис. 7.39). Назовите вершины куба, симметричные относительно его центра.
Ответ:
Симметричные вершины куба относительно его центра следующие:
- А и C1;
- D и B1;
- A1 и C;
- B и D1.
Это означает, что для каждой пары вершин куба, если провести прямую через центр куба, эти вершины будут симметричны относительно этой прямой. Все они расположены на одинаковом расстоянии от центра куба.
Решение:
Куб является пространственной фигурой с восьмью вершинами, двенадцатью рёбрами и шестью гранями. Центр симметрии куба — это точка, которая находится в центре геометрической фигуры и является симметричной относительно всех её точек, если провести соответствующие отражения. Вершины куба, которые находятся на одинаковом расстоянии от центра, могут быть симметричными относительно этого центра. Для куба есть несколько пар таких симметричных вершин.
Вершины куба, симметричные относительно его центра, следующие:
- A и C1: Эти две вершины противоположны друг другу и симметричны относительно центра куба. Если провести прямую через центр куба, эти вершины будут находиться на одинаковом расстоянии от этой прямой.
- D и B1: Эти вершины также симметричны относительно центра куба, и их расположение зеркально отражается друг в друге через центр куба.
- A1 и C: Вершины A1 и C также симметричны относительно центра куба. Эти вершины противоположны друг другу, и если провести прямую через центр куба, они будут зеркальными отражениями друг друга относительно этой прямой.
- B и D1: Аналогично, эти вершины симметричны относительно центра куба и могут быть отражены относительно центра, образуя зеркальную пару.
Ответ: Вершины куба, симметричные относительно его центра: A и C1, D и B1, A1 и C, B и D1.
Таким образом, все эти вершины находятся на одинаковом расстоянии от центра куба, и для каждой пары существует соответствующее отражение, которое создаёт симметричные фигуры. Этот принцип используется при построении и анализе геометрических фигур, чтобы лучше понять их симметричные свойства и особенности.
