Учебник по математике для 6-го класса авторов Дорофеева и Шарыгина — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
Что выделяет этот учебник среди других:
- Понятное изложение материала. Каждая тема объясняется простым и доступным языком, что облегчает понимание даже сложных понятий.
- Большое количество примеров и задач. Учебник предлагает разнообразные упражнения — от простых до более сложных, что помогает закрепить пройденный материал.
- Интерактивный подход. В книге есть задания, которые побуждают учеников к самостоятельному поиску решений и развитию творческого мышления.
- Связь с реальной жизнью. Многие задачи связаны с практическими ситуациями, что делает математику более живой и понятной.
- Разнообразие форм подачи информации. Здесь используются таблицы, схемы, иллюстрации, что помогает лучше усваивать материал и удерживать внимание учащихся.
ГДЗ по Математике 6 Класс Номер 592 Дорофеев, Шарыгин — Подробные Ответы
Исселедуем.
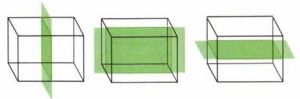
У параллелепипеда три плоскости симметрии (см. рис. 7.19). А сколько плоскостей симметрии у куба?
Указание. Рассмотрите дополнительно плоскости, проходящие через диагонали противоположных граней.
У куба девять плоскостей симметрии, так как три плоскости проходят через середины противоположных рёбер и шесть плоскостей проходят через противоположные рёбра.
Это означает, что куб имеет симметричные плоскости, которые делят его на две одинаковые части. В кубе есть три плоскости симметрии, которые делят его через середины противоположных рёбер, и шесть плоскостей симметрии, которые проходят через противоположные рёбра, что придаёт кубу высокую степень симметрии. Таким образом, куб является одним из геометрических объектов, обладающих богатой симметрией.
У куба девять плоскостей симметрии, так как три плоскости проходят через середины противоположных рёбер и шесть плоскостей проходят через противоположные рёбра.
Это важное свойство куба, поскольку оно объясняет, как можно разделить куб на две одинаковые части, которые будут симметричны относительно указанных плоскостей. Куб является одним из наиболее симметричных трёхмерных объектов в геометрии, и его симметрия проявляется в различных аспектах, таких как форма и расположение рёбер, граней и вершин.
Рассмотрим подробнее:
- Три плоскости симметрии проходят через середины противоположных рёбер. Эти плоскости делят куб на две одинаковые части, и каждая из них может быть расположена перпендикулярно двум другим рёбрам куба. Это объясняет, почему куб обладает высокой степенью симметрии: при отражении относительно этих плоскостей куб сохраняет свою форму.
- Шесть плоскостей симметрии проходят через противоположные рёбра. Эти плоскости также разделяют куб на две равные части, но они проходят вдоль рёбер куба. Эти плоскости также демонстрируют высокую степень симметрии куба, так как отражение куба относительно таких плоскостей также не изменяет его внешнего вида, и каждая часть остаётся идентичной.
Куб, как правильный многогранник, обладает замечательной симметрией, и это свойство широко используется в различных областях, таких как архитектура, искусство, и даже в науке для моделирования идеальных объектов. Симметрия куба позволяет легко анализировать его характеристики и применять его в практических задачах, где требуются такие свойства, как равенство сторон и углов, а также высокая степень симметрии.
Таким образом, куб является ярким примером объекта с уникальной и четкой симметрией, что делает его особенно важным в геометрии и других областях науки.
