Учебник по математике для 6-го класса авторов Дорофеева и Шарыгина — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
Что выделяет этот учебник среди других:
- Понятное изложение материала. Каждая тема объясняется простым и доступным языком, что облегчает понимание даже сложных понятий.
- Большое количество примеров и задач. Учебник предлагает разнообразные упражнения — от простых до более сложных, что помогает закрепить пройденный материал.
- Интерактивный подход. В книге есть задания, которые побуждают учеников к самостоятельному поиску решений и развитию творческого мышления.
- Связь с реальной жизнью. Многие задачи связаны с практическими ситуациями, что делает математику более живой и понятной.
- Разнообразие форм подачи информации. Здесь используются таблицы, схемы, иллюстрации, что помогает лучше усваивать материал и удерживать внимание учащихся.
ГДЗ по Математике 6 Класс Номер 590 Дорофеев, Шарыгин — Подробные Ответы
Ищем способ построения.
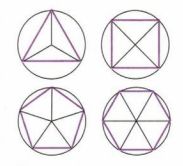
Правильные многоугольники обладают важным свойством: все вершины правильного многоугольника лежат на одной окружности (рис. 7.27). Это свойство можно использовать для построения правильного многоугольника: разделить окружность на соответствующее число равных частей (равных дуг) и соединить последовательно точки деления.
1) Рассмотрите рисунок, сформулируйте алгоритм построения:
а) правильного треугольника;
б) правильного четырёхугольника.
Выполните построения.
2) Выберите один из двух других изображённых на рисунке правильных многоугольников и постройте его.
1) Построение правильных многоугольников:
- Алгоритм построения правильного треугольника:
- Разделите окружность на шесть равных частей, шаг циркуля равен её радиусу;
- Соедините полученные точки через одну.
- Алгоритм построения правильного четырёхугольника:
- Проведите два взаимно перпендикулярных диаметра окружности;
- Соедините полученные точки пересечения по порядку.
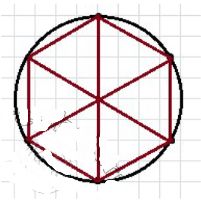
2) Нарисуем правильный шестиугольник:
- Для построения правильного шестиугольника, разделите окружность на шесть равных частей и соедините точки деления. Таким образом, получится шестиугольник, у которого все стороны и углы одинаковы.
Выберите один из двух других изображённых на рисунке правильных многоугольников и постройте его:
- Правильный треугольник: разделите окружность на 3 равные части и соедините точки.
- Правильный четырёхугольник (квадрат): разделите окружность на 4 равные части и соедините точки.
1) Построение правильных многоугольников:
- Алгоритм построения правильного треугольника:
- Нарисуйте окружность с центром в любой точке на листе бумаги.
- Теперь разделите окружность на шесть равных частей, шаг циркуля равен её радиусу. Это можно сделать, проведя несколько равных дуг от центра окружности. Для этого используйте транспортир или циркуль, чтобы точно разделить круг на 6 одинаковых частей.
- После того как вы разделите окружность на шесть частей, соедините каждую вторую точку, чтобы получился правильный треугольник. В итоге получится равносторонний треугольник, так как все его стороны будут одинаковыми.
- Алгоритм построения правильного четырёхугольника (квадрата):
- Начертите окружность с центром в любой точке на листе.
- Проведите два взаимно перпендикулярных диаметра окружности, которые пересекаются в центре окружности. Эти диаметры должны разделить окружность на 4 равные части.
- После того как диаметры будут проведены, вы получите 4 точки на окружности. Соедините эти точки прямыми линиями по порядку, чтобы получить правильный четырёхугольник, то есть квадрат. Все стороны квадрата будут равными, а углы прямыми (90 градусов).
2) Нарисуем правильный шестиугольник:
- Для построения правильного шестиугольника, начните с того, что нарисуйте окружность. Затем разделите её на шесть равных частей. Для этого можно воспользоваться циркулем или углом, чтобы делить окружность на равные дуги.
- После того как окружность будет разделена, поставьте точки на каждом из делений. Соедините эти точки прямыми линиями по порядку, и у вас получится правильный шестиугольник. Все его стороны будут одинаковыми, а углы между соседними сторонами равными.
- Правильный шестиугольник также имеет важную особенность: если провести одну из его диагоналей, то она будет перпендикулярна соседним сторонам. Это также характерно для правильных многоугольников.
Теперь вы можете выбрать один из двух других многоугольников, изображённых на рисунке, и построить его, следуя аналогичным шагам:
- Для правильного треугольника: разделите окружность на 3 равные части и соедините точки, получив равносторонний треугольник.
- Для правильного четырёхугольника (квадрата): разделите окружность на 4 равные части, проведите два диаметра, и соедините точки пересечения по порядку, чтобы получить квадрат.
Этот метод построения правильных многоугольников на окружности даёт вам возможность легко и точно создавать геометрические фигуры, все вершины которых лежат на одной окружности. Такой подход также помогает лучше понять свойства правильных многоугольников, таких как одинаковые стороны и углы.
